��b���_(1)
��b���_
���U���w
�E�f�[�^�ʂȂǂ���������
�E�R���s���[�^�̗��_��H��f�[�^�\���A���ꗝ�_�Ȃǂ̊�b
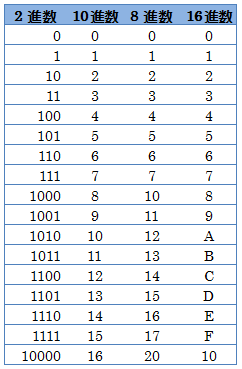
2�i���E10�i���E8�i��16�i��
2�i���F�R���s���[�^�����ł̓d���̗L���Ȃǂ�
�@�@�@�@�@�@�@����Ď��ʂ��ꂽ�f�[�^
�@�@�@�@�@�@�@�u0�v�Ɓu1�v�ŕ\��
10�i���F�ʏ�̐������g�p�����\��
�@�@�@�@�@�@�@0�`9�̐���
8�i���F�R���s���[�^�ň������ʂ̕\�����@
�@�@�@�@�@�@�@0�`7�̐���
16�i���F�R���s���[�^�ň������ʂ̕\�����@
�@�@�@�@�@�@�@0�`9�̐����{a�`f�̃A���t�@�x�b�g
�
���ʂ�\������ۂɁA�ʎ��̊�ƂȂ鐔�̂���
10�i���F10�{���ƂɌ����オ��A���10
2�i���@�F���2�A2�{���ƂɌ����オ���Ă���
16�i���F���16�A16�{���ƂɌ����オ��A
�@�@�@�@�@�@�@�u1�A16�A256�A�`�̈ʁv�ƂȂ�
 ���̏d��
���̏d��
10�i���Ȃ牺�ʌ�����1,10,100,1000,�`�ƁA�����オ�邲�Ƃ�10�{����A2�i���ł͉��ʌ�����1,2,4,8,�`�ƁA�����オ�邲�Ƃ�2�{�����B���ꂪ�u���̏d�݁i�����݁j�v
��ϊ�
����i������ʂ̐i���ɒu�������邱��
n�i����10�i��
���̏d�݂Ɍ��ɏ����ꂽ���l(n)���|���A���̌��ʂ������ĉ��Z����
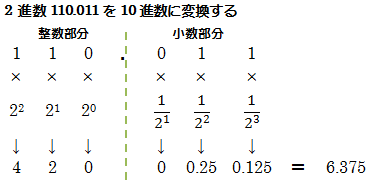
10�i����n�i��
�������F10�i����n�Ŋ����ď��Ɨ]������߁A����1�ɂȂ�܂ŌJ��Ԃ��A
�@�@�@�@���߂��]���1�����ʌ�������ׂ�
�������F10�i����n���|���āA��������0�ɂȂ�܂ŌJ��Ԃ��A
�@�@�@�@���������ォ��L�q����
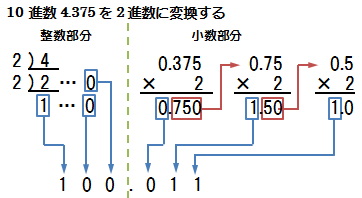
 ��������
��������
10�i���̏�������2�i���ɕϊ����A2���|�������Z���ʂ̏�������0�ɂȂ�Ȃ������B
(��F(0.1)10��(0.00011001100�c)2�@�̂�(0.1)10�͖�������)
���������F�悸�����ɂ��āA2�̗ݏ�݂̂̐����ō\������Ă�����L������
2�i����8�i���E16�i��
�����_����_�ɂ��āA8�i���ł����3�����ƁA16�i���ł����4�����Ƃɋ��
�������͉E�����ɁA�������͍����E�ɋ��A���ꂼ���8�i��or16�i���ɕϊ�
��3��(8�i��)�A4��(16�i��)�ɂȂ�Ȃ��ꍇ�́A�s�����Ă��錅���Ԃ�0���[����
8�i���E16�i����2�i��
1������2�i���ɕϊ����A�L�q����
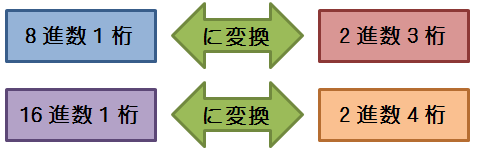
| 2�i����8�i���F3���ɋ���āA2�i���̌��̏d�݂��|���đ��� 2�i����16�i���F4���ɋ���āA2�i���̌��̏d�݂��|���đ��� n�i����10�i���Fn�i���̊e���̐��l�ƌ��̏d�݂��|���đ��� �@�@�@�@�@�@�@(�������A����������) 10�i����n�i���F10�i����n�Ŋ���A�]������ʌ�������ׂ�(������) �@�@�@�@�@�@�@�F10�i����n���|���ď�������0�ɂȂ�܂ŌJ��Ԃ��A �@�@�@�@�@�@�@�@���������ォ��L�q(������) |
�����̕\��
�R���s���[�^�ł͕�����2�i���̐��l�Ƃ��Ĉ����Ă���B�R���s���[�^��ň��������Ɋ���^����ꂽ2�i���R�[�h���u�����R�[�h�v�ƌĂ�ł���B���Ăł�1�o�C�g�ō\�����邪�A���{�ł͂Ђ炪�ȁE�J�^�J�i�E�����Ȃǂ̕��������p���邽��2�o�C�g�ŃR�[�h������Ă���
��\�I�ȕ����R�[�h
| ���� | ���� |
|---|---|
| ASCII | ANSI(�č��K�i����)���K�i���������R�[�h�B1�o�C�g�����B1�����ɂ�7�r�b�g���g�p���A8�r�b�g�ڂ̓G���[�m�F�p�̃p���e�B�B������������щ����L�� |
| JIS | JIS(���{�H�ƋK�i)���K�i���������R�[�h�B�p�����E�L���Ȃǂ�1�o�C�g�����ƂЂ炪�ȁA��������2�o�C�g�������܂� |
| �V�t�gJIS | JIS�̈��BMicrosoft�ɂ���Ē�`���ꂽ�BWindows��Mac OS�Ȃǂō̗p����Ă���A�����ōł����y |
| EUC | AT&T�Ђ��K�i�B�g��UNIX�R�[�h�Ƃ������B���UNIX�ŗ��p����Ă���B2�o�C�g�����ɂ��Ή� |
| EBCDIC | �č�IBM�Ђ��K�i�B8�r�b�g�̕����R�[�h�B��ɔėp��^�R���s���[�^�ō̗p |
| Unicode | ISO��IEC���K�i�B�S���E�̕�����2�o�C�g�ŕ\�����邱�ƂŁA1�̃R�[�h�łقƂ�ǂ̕��������^ |
 �p���e�B�r�b�g
�p���e�B�r�b�g
�����R�[�h�Ȃǂ̌����������邽�߂̃r�b�g�̂���
�r�b�g�ƃo�C�g
�R���s���[�^�Ŏ�舵����f�[�^�́A�r�b�g(binary digit:bit)�ƃo�C�g(byte)�Ƃ����P�ʂŎ�舵���A�r�b�g�̓R���s���[�^�����ɂ�������\���̍ŏ��P�ʂŁA1�r�b�g�ł�"0"�܂���"1"���i�[�����
�f�[�^�̋L���e�ʂȂǂ�\���Ƃ��ɗp������
| �E�r�b�g�̓R���s���[�^�����ɂ�������\���̍ŏ��P�� �E�f�[�^�̗e�ʂ�\���P�� �E1�r�b�g�ł�"0"�܂���"1"���i�[����� �E8�r�b�g��1�o�C�g |
���l�̕\��
�R���s���[�^��̌���ꂽ�r�b�g���Ő��l��\�����邽�߂̕\�����@�ɂ͈ȉ��̂��̂�����
10�i���̕\�����@
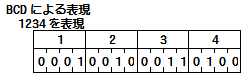
 BCD�@(2�i��10�i)
BCD�@(2�i��10�i)
2�i��4����p���āA10�i���ɂ�����1������\��������@
�y�����z
�������̕�����\���ł��Ȃ�
���{���A2�i����4�����g�p�����16��ނ��\���\�����ABCD�ł�0�`9��10���
�@��\��������
��10�i���ɂ����Č���1�����邲�ƂɁABCD�ł�4�������邱�ƂɂȂ�
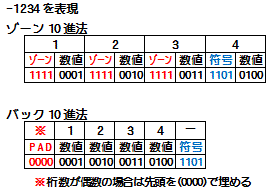
 �]�[��10�i���@(�A���p�b�N10�i��)
�]�[��10�i���@(�A���p�b�N10�i��)
1���̐��l��1�o�C�g(8�r�b�g)�ŕ\�����@
1�o�C�g�̏��4�r�b�g���]�[�����Ƃ����AJIS�R�[�h�̏ꍇ��0011�AEBCDIC���[�ǂ̏ꍇ��1111���ݒ肳���
1�o�C�g�̊K�r�b�g�����l��\��
�ʼn��ʌ��̃]�[�����͐����̕�����\��(���F1100�A���F1101�Ƃ��邱�Ƃ�����)
�y�����z
��1�o�C�g�ł��̐��l�̕����R�[�h��\��
�����l�ƕ����̕ϊ����ȒP�ɍs����
 �p�b�N10�i��
�p�b�N10�i��
1���̐��l��4�r�b�g�ŕ\�����@
�ʼn��ʌ���4�r�b�g�͐����̕�����\��(���F1100�A���F1101�Ƃ��邱�Ƃ�����)
�����������̂Ƃ��́A���[��0000�����A�f�[�^�𐮐��o�C�g�ŕ\����悤�ɂ���
�y�����z
���]�[��10�i���Ɣ�r���āA�K�v�Ȍ��������Ȃ��Ă���
�����̕\�����@
 ��Βl�\��
��Βl�\��
��Βl�\���́A��ԍ��[�̃r�b�g�ł����ŏ�ʂ̃r�b�g���r�b�g�ɂ������̐��l�ł����0�A���̐��l�ł����1���Z�b�g����
 �␔�\��
�␔�\��
 �␔�Ƃ�
�␔�Ƃ�
���鐔�l�̌����ЂƂJ��グ�邽�߂ɉ��Z���鐔�l�̂���
(��F10�i���ł�6�{4��10�ł��邩��6�̕␔��4)
 1�̕␔
1�̕␔
���鐳�̐���\���r�b�g������ׂĔ��]�������\���`��]
����̐��Ƃ��Ē�`����
1�̕␔�̌��_�F0��00000000��11111111�Ƃ�����ʂ�̕\���`��������
 2�̕␔
2�̕␔
���鐳�̐���\���r�b�g������ׂĔ��]�����A1�����Z�����\���`��(1�̕␔�ŕ\���ꂽ����1������������)�̐��Ƃ��Ē�`����
0����ʂ�ɕ\���������͏��ł���
2�̕␔�̍ő�̃����b�g�͑����Z���s���Ƃ��Ƀv���X�ł��邩�}�C�i�X�ł��邩�ɂ���ďꍇ���������Ȃ��čςނ���
 2�i���̌��Z
2�i���̌��Z
2�̕␔���g�p���邱�ƂŁA2�i���̌��Z�����Z�Ƃ��Čv�Z�\
 �\���\�Ȑ��l�͈̔�
�\���\�Ȑ��l�͈̔�
2�̕␔�̏ꍇ�An�r�b�g�ŕ\���\�Ȑ��l�͈̔́F�|2n-1�`2n-1�|1
| 1�̕␔�̋��ߕ� �@�@�@�@�e����1��0�]���� 2�̕␔�̋��ߕ� �@�@�@�@1�̕␔�{1 �}�C�i�X��10�i����2�̕␔�\������ �@�@�@�@10�i����2�i���ɕϊ����A����2�i����2�̕␔�\������ 2�̕␔�\�����ꂽ�}�C�i�X��2�i����10�i���ɕϊ����� �@�@�@�@�ŏ�ʃr�b�g�ɒ��ڂ��āA �@�@�@�@�@�@1�Ȃ�}�C�i�X������2�̕␔�����߂� �@�@�@�@�@�@�O�Ȃ���̂܂�2�i����10�i���ɕϊ����� |
�����̕\�����@
 �Œ菬���_��
�Œ菬���_��
�����_�̈ʒu�����̈ʒu�ɌŒ肵�Đ��l��\��������@
���\���ł���l�͈̔͂��͂邩�ɋ���
�����������N����Ȃ�
�������ɉ��Z�\
�������Ȃ��Œ菬���_���F���̐���\���ł��Ȃ�
�������t���Œ菬���_���F�ŏ�ʂ̃r�b�g�������̕����r�b�g�ɂȂ�
 ���������_��
���������_��
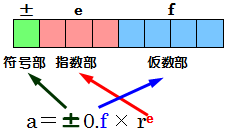
�����_�̈ʒu���ړ����A���ڍׂȐ��l������������@
��ʓI�ɃR���s���[�^�Ȃǂ́A�������Ə��������Đ��l�Ǘ����s���A�������̃f�[�^�\���ɂ����ĕ��������_����p���Ă���
���������_���ł́A����a���ua��0.f�~re�v(f�������Ae���w���Ar���)�Ƃ����`�ŕ\������
| ���� | ���� |
|---|---|
| ������ | ���l������������\���B���̏ꍇ0�A���̏ꍇ1 |
| �w���� | ��ׂ̂����2�i���ŕ\���B���ׂ̂����2�̕␔���g�p |
| ������ | �����_�ȉ��̐��l��\���B���K�����Ă��� |
 ���������_���̐��K��
���������_���̐��K��
�����_�̒����0�ȊO�̐��l�����Ԃ悤�ɒ������ĕ\�����邱��
(��F0.0023578��0.23578�~10-2)
 �␔���̃r�b�g
�␔���̃r�b�g
���������_���̎w�����̃r�b�g�͈�ʓI��2�̕␔��p����ꍇ�Ɓu�G�N�Z�X�v�ƌĂ���@���g���ĕ\������ꍇ������
���G�N�Z�XN�w�����̕��̐��l�𐳂̐��l�ɒu�������邽�߂�63��127�ȂǁA���̐��l�����Z���Ă���r�b�g�\��������
 �P���x���������_��
�P���x���������_��
1�̐��l��32�r�b�g�ŕ\�����镂�������_���^
��ʓI�ɁA1�r�b�g�̕������A7�r�b�g�̎w�����A24�r�b�g�̉�������32�r�b�g�ŕ\������B�\���ł���l�͈̔́|3.40282�~1038�`3.40282�~1038�ŁA���x��6���AC����Ȃǂł́ufloat�^�v�ȂǂƌĂ�Ă���
 �{���x���������_��
�{���x���������_��
1�̐��l��64�r�b�g�ŕ\�����镂�������_��
��ʓI�ɁA1�r�b�g�̕������A11�r�b�g�̎w�����A52�r�b�g�̉������̌v64�r�b�g�ŕ\������B�\���ł���l�͈̔͂́|1.79769�~10308�`1.79769�~10308�ŁA���x��15��
�덷
�R���s���[�^��Ő��l�\���Ɏg�p�ł���r�b�g�������܂��Ă��邽�߁A���Z���ʂɎ��ۂ̐��l�ƃR���s���[�^�ŕ\�����鐔�l�̍��u�덷�v��������
�ۂߌ덷
�����_�ȉ��̋ɂ߂ď������P�ʂŒl���ۂ߂Čv�Z�������ʁA�v�Z���ʂƐ������l���킸���ɂ���邱��
�ʼn��ʌ���菬�����������l�̌ܓ���؎̂āA��グ���s���Ƃ��ɐ�����덷
��������
���������_���Z�ŁA�v�Z���ʂ�0�ɋɒ[�ɋ߂��Ȃ�����Z���s�����Ƃ��ɁA�L�������̌������ɒ[�ɏ��Ȃ��Ȃ邱��
(��F�u0.123456x102-0.123455x102�v�̂悤�Ȍv�Z���s���ƁA�u1x10-4�v�ƂȂ�A�L�������̌�����7�������C��1���Ɍ������Ă��܂�)
���������_�`���ł͏�ɗL�������̌��������ɂ��Ĉ����Ă��邽�߁A�����������ɕs�����������������I��0�Ŗ��߂Ă��܂��A�^�̒l�Ƃ̊ԂɌ덷���������Ă��܂��B���̒l���v�Z�Ɏg�p���邱�Ƃő傫�Ȍ덷���܂l���Ԃ���邱�Ƃ�����
���
��Βl�̑傫�����ɒ[�ɈقȂ鐔���̉��E���Z���ɏ������l�̏��������邱�ƁB���̂��Ƃɂ���ċN����v�Z�̌덷
�傫�����ɒ[�ɈقȂ�l�𑽐��v�Z����ꍇ�A����̉e���œK�Ȍv�Z���ʂ������Ȃ����Ƃ����邽�߁A�H�v�K�v�ƂȂ�
�I�[�o�[�t���[(�����ӂ�)
���l���Z���s�������ʂ̐�Βl���A�����鐔�l�̍ő�l���邱��
��̐��l��\�����邽�߂Ɋ��蓖�Ă�ꂽ�L���e�ʂ̏���������
�A���_�[�t���[
���������_���Z�����ŁA�v�Z���ʂ̎w���������������Ȃ�߂��A�g�p���Ă���L�q���@�ł͐��l���\���ł��Ȃ��Ȃ���

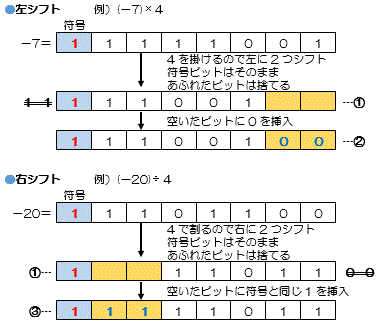
�V�t�g���Z
�r�b�g�̈ʒu������E�ɂ��炷���ƂŁA���l�̏�E���Z�������ɏ���������@
| �����ɂ��炷(���V�t�g):���̐��l��2��n��{(2��n��ŏ�Z) ���E�ɂ��炷(�E�V�t�g):���̐��l��2�́|n��{(2��n��ŏ��Z) |
�Z�p�V�t�g
�������l���������l���Z���s�����Ɏg�p
a)�����r�b�g�������r�b�g����V�t�g����@---�@
b)�͂ݏo�����r�b�g�͐�̂Ă�@---�@
c)���r�b�g�ʒu�ɂ�
�@�@�@�@���V�t�g�F"0"�@---�A
�@�@�@�@�E�V�t�g�F�����r�b�g�Ɠ����l�@---�B
�@�@���i�[����
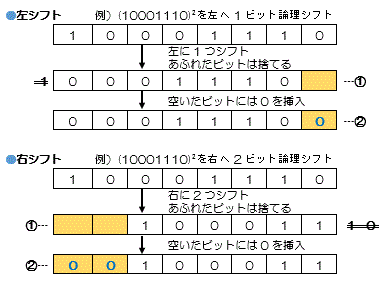
�_���V�t�g
���l���Z�ł͂Ȃ��A�P�Ƀr�b�g�̈ʒu���ړ�����Ƃ��Ɏg�p
a)�����r�b�g���܂ނ��ׂẴr�b�g����V�t�g����@---�@
b)�͂ݏo�����r�b�g�͐�̂Ă�@---�@
c)���r�b�g�ʒu�ɂ�"0"���i�[����@---�A
�W���Ƙ_�����Z
�W���F��������Ɋ�Â��ăO���[�v�����ꂽ�f�[�^�̏W�܂�̂��ƂŁuA�܂���B�v�Ȃǂ̕��͂ŕ\���\�B���̂悤�ȕ��͂������(�_����)�Ƃ����B�x���}�ɂ��}�������邱�Ƃ��\
�_�����Z�Ƙ_����H
�_�����Z�F�����̏���(�_��)�̑g�ݍ��킹���������ŕ\�������̉��Z���@
�_����H�F�R���s���[�^�����̘_�����Z��S������d�q��H
�@�@�@�@�@�@�u��H�L��(MIL�L��)�v���g���Đ}�ŕ\������
 �_���L��
�_���L��
�_�����Z���s���Ƃ��Ɏg����L��
| �_���L�� | �Ӗ� | �� |
|---|---|---|
| �E�@,�@�� | �_����(AND) | X�EY�@,�@X��Y |
| �{�@,�@�� | �_���a(OR) | X�{Y�@,�@X��Y |
| �\�@,�@�� | �ے�(NOT) | X�@,�@��X |
| �r���I�_���a(EOR,XOR) | X |
 ������H�Ƒg�ݍ��킹��H
������H�Ƒg�ݍ��킹��H
�_����H�́u������H�v�Ɓu�g�ݍ��킹��H�v�ɕ��ނ����
 ������H
������H
���͒l�Ƙ_����H�̓�����Ԃɂ���ďo�͂����܂�_����H
�t���b�v�t���b�v��H
 �g�ݍ��킹��H
�g�ݍ��킹��H
�_����H�̓�����ԂƂ͊W�Ȃ��A���͒l�����ɂ���ďo�͂����܂�_����H
 �t���b�v�t���b�v��H
�t���b�v�t���b�v��H
�u0�v�Ɓu1�v�̂ɂ����1��H��1�r�b�g�̏����ꎞ�I�ɋL���ł���_����H�̂���
 ��{�I�Ș_�����Z
��{�I�Ș_�����Z
| ���� | ���� | ��H�L�� |
|---|---|---|
| �_����(AND) | 2�̓��͒l���Ƃ���1�̂Ƃ�1�A ����ȊO��0���o�� |  |
| �_���a(OR) | 2�̓��͒l���Ƃ���0�̂Ƃ�0�A ����ȊO��1���o�� |  |
| �ے�(NOT) | ���͒l��1�Ȃ��0�A 0�Ȃ��1���o�� |  |
| �@ | �_���� | �_���a | �ے� | |
|---|---|---|---|---|
| AND | OR | NOT | ||
| �@X | �@Y | X�EY | X�{Y | X |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 |
 �g�����̘_�����Z
�g�����̘_�����Z
| ���� | ���� | ��H�L�� |
|---|---|---|
| �ے�_���� (NAND) | �_���ςƔے��g�ݍ��킹���_�����Z 2�̓��͒l���Ƃ���1�̂Ƃ�0�A ����ȊO��1���o�� |  |
| �ے�_���a (NOR) | �_���a�Ɣے��g���킹���_�����Z 2�̓��͒l���Ƃ���0�̂Ƃ�1�A ����ȊO��0���o�� | 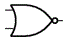 |
| �r���I�_���a (EOR�@,�@XOR) | �_����t�Ƙ_���a�Ɣے��g���킹���_�����Z 2�̓��͒l�������Ȃ�0�A �قȂ�Ȃ�1���o�� | 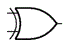 |
| �@ | �ے�_���� | �ے�_���a | �r���I�_���a | |
|---|---|---|---|---|
| NAND | NOR | EOR�@,�@XOR | ||
| �@X | �@Y | X�EY | X�{Y | X��Y |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 |
 �_�����Z�̖@��
�_�����Z�̖@��
 �h�E�����K���̖@��
�h�E�����K���̖@��
| 1)�_���a�̔ے�́A�ے�̘_���ςɓ����� |
 ���z��
���z��
| A�E(B�{C)��A�EB�{A�EC A�{(B�EC)��(A�{B)�E(A�{C) |
 �_���ς̖@��
�_���ς̖@��
| A�EA��0 A�E0��0 A�E1��A |
 �_���a�̖@��
�_���a�̖@��
| A�{A��1 A�{0��A A�{1��1 |
 �v��H(��H�v)
�v��H(��H�v)
�_����H��g���킹�Ď��ۂɕK�v�ȉ�H�̍\����_���I�ɐv���邱��
���\�A���쐫�A�M�����A�v������R�X�g�̍팸���܂߂Đv����
�����Z��ƑS���Z��
�l���v�Z��_�����Z���s����H���u���Z��H�v�Ƃ����A2�i���̉��Z���s�����Z��H���u���Z��v�Ƃ����B���Z��ɂ́u�����Z��v�Ɓu�S���Z��v������
 �����Z��
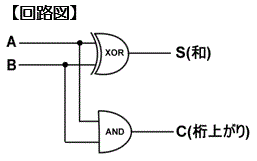
�����Z��
2�i���̉��Z�ʼn��ʌ�����̌��オ����l�����Ȃ����Z��̂���
�_���ςƔr���I�_���a�̉�H�̑g�ݍ��킹�ō\�������
�y�����z
��2�i���̉��Z���s�����߂́A�ʼn��ʂ̃r�b�g���Z
�������Z���2�r�b�g�ȏ�̌��������Z�ɂ͎g�p�ł��Ȃ�
| ���� | �o�� | ||
|---|---|---|---|
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
 �S���Z��
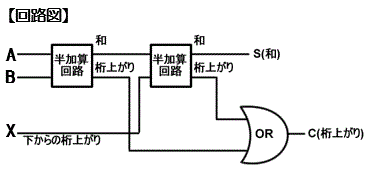
�S���Z��
2�i���̉��Z�ʼn��ʂ̌�����̌��オ����܂߂���Z��̂���
2�̔����Z��Ƙ_���a�̉�H�̑g�ݍ��킹�ō\�������
�y�����z
�������Z���2�r�b�g�ȏ�̂����������Z�ɂ͎g�p�ł��Ȃ�
| ���� | �o�� | |||
|---|---|---|---|---|
| A | B | X | C | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |

