基礎理論(5)
アルゴリズムとプログラミング
アルゴリズム
ある問題を解くための一連の処理手順。処理の手順が必ずしも1通りではない場合、アルゴリズムによって手順の明確化を行い、プログラムを効率よく作成することが出来る
アルゴリズムの表現
流れ図(フローチャート)
作業の流れやプログラムの手順を記号や矢印などを使って図で表したもの
流れ図には日本工業規格(JIS規格)によって定められた記号が用いられ、プログラム手順だけでなくデータの経路や制御を示すことも可能
| 記号 | 名称 | 説明 |
|---|---|---|
 | 端子 | 流れ図の始まりと終わり |
 | 線 | 手順、データ、制御の流れ |
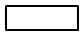 | 処理 | 演習や代入の処理 |
 | 定義済み処理 | 定義済みの処理を記載 |
 | データ記号 | データの入出力 |
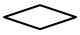 | 判断 | 条件を判断して、処理から一つを選択する制御機能 |
 | ループ端(開始) | 繰り返し処理の前で条件を判断する場合、繰り返し処理の終わる条件を記載 |
 | ループ端(修了) | 繰り返し処理のあとで条件を判断する場合、繰り返し処理の終わる条件を記載 |
 トレース表
トレース表
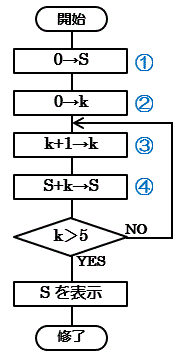
トレース:流れ図の繰り返し処理などが行われる際に、
変数の値を追跡すること。
スレースの結果を表示した表を「トレース表」という
左の流れ図をトレースすると
| 手順 | k | S |
|---|---|---|
| ① | - | 0 |
| ② | 0 | 0 |
| ③ | 1 | 0 |
| ④ | 1 | 1 |
| | | | | | |
擬似言語
プログラムの設計段階で、簡単な記号を使って処理の流れを表現できる言語のこと。擬似言語で書かれたアルゴリズムは、宣誓部と処理部で構成される
詳細は後述の擬似言語を参照
決定表(デシジョンテーブル)
条件と処理の関係をまとめた表のこと。複雑な条件判断のもと、処理を決定するときに利用される
| 条件1 | Y | Y | N | N |
|---|---|---|---|---|
| 条件2 | Y | N | Y | N |
| 処理1 | X | X | X | - |
| 処理2 | - | - | - | X |
※条件--Y:条件を満たす N:条件を満たさない
※処理--X:処理を実行する -:処理を実行しない
アルゴリズムの基本構造
アルゴリズムの基本構造には「順次構造」「選択構造」「繰り返し構造」がある
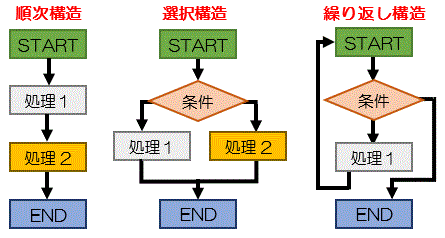
順次構造
順番に流れを示したもの
選択構造
条件によって処理が選択される
繰り返し構造
決められた回数または条件などによって、条件が満たされている間、または条件が満たされるまで、同一の処理が繰り返される
代表的なアルゴリズム
探索のアルゴリズム
探索(検索)(サーチ):与えられた条件に合致するデータを探すこと
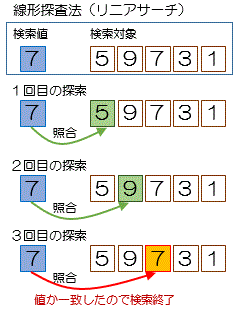
線形探索法(リニアサーチ、順次探索法)
配列に格納されているデータを先頭から末尾まで順番に探していくアルゴリズムのこと
※この探索方法は配列内に目的のデータが存在する
ことを前提とした場合にのみ成立する
そのため、配列内に目的データが存在しない場合
を想定し、探し出す前に目的データを配列の最後
に追加しておく。この処理のことを「番兵法」と
いう
(例)番兵法を使って配列a[1]~a[n]に格納された
データから目的のデータ「x」を探し出すときの
アルゴリズム
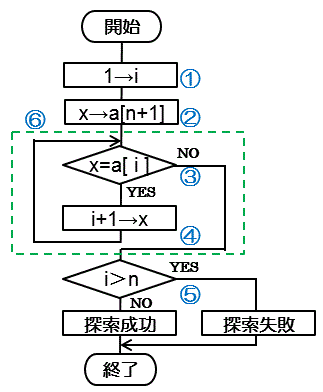
| ① | データの位置格納変数 i に1を代入 |
| ② | 配列の最後に目的のデータを代入(番兵法) |
| ③ | 配列の値と目的の値を比較 |
| ④ | 正しくなければ i +1 |
| ⑤ | i がnより大きくなければ検索成功 i がnより大きければ検索失敗 |
| ⑥ | 繰り返す |
配列にn個のデータがある場合 最短:1回 最大:n回 平均:(n+1)/2回 |
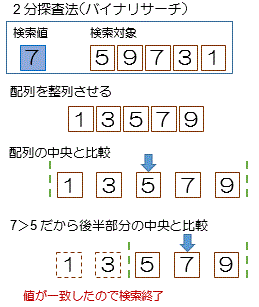
2分探索法(バイナリサーチ)
対象が、データ群の中央にあるデータより前にあるか、後ろにあるかを判断し、2分したデータ群を取捨選択する。更に、残ったデータ群の中央から前後のどちらにあるかを判断し、取捨選択を繰り返して絞り込んでいく。データを昇順に整列させておく必要がある
(例)2分探索法を使用し、配列a[1]~a[n]に格納さ
れたデータから目的のデータ「x」を探し出すと
きのアルゴリズム
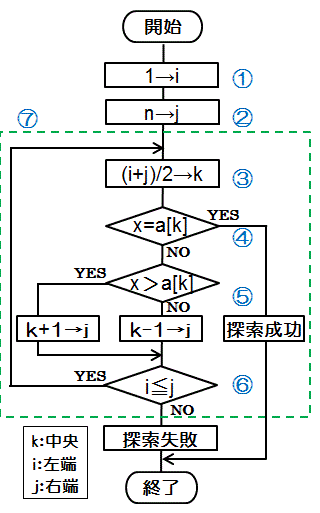
| ① | 左端位置格納変数 i に1を代入 |
| ② | 右端位置格納変数 j にnを代入 |
| ③ | 中央位置格納変数 k に「(i+j)/2」を代入 |
| ④ | 目的のデータと中央位置のデータを比較 |
| ⑤ | 目的のデータが中央位置データより大きい場合i に「k+1」を代入 目的のデータが中央位置データより小さい場合i に「k-1」を代入 |
| ⑥ | i≦jの間、処理を繰り返す |
| ⑦ | 繰り返す |
配列にn個のデータがある場合 最短:1回 最大:log2n+1回 平均:log2n回 |
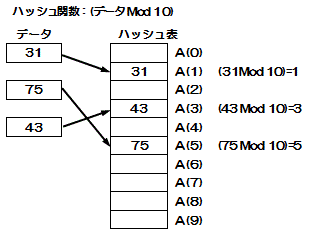
ハッシュ表探索法
データを格納するときにあらかじめ関数を使ってデータの格納位置を決め、データを探し出すときに同じ関数を使って格納位置を算出するアルゴリズム
ハッシュ値(ハッシュキー):データの格納位置
ハッシュ関数:ハッシュキーを決めたり探し出したりする関数
ハッシュ表:データを格納した表
 ハッシュ表におけるシノニム
ハッシュ表におけるシノニム
ハッシュ表検索法では、ハッシュキーが同じ場合、ハッシュ表にデータを格納する際にデータ同士の衝突が発生する。このデータの衝突を「シノニム」という
整理のアルゴリズム
 整列(並べ替え・ソート)
整列(並べ替え・ソート)
一定の規則のもとにデータを昇順や降順に並べ替えること
| データ | 昇順 |
|---|---|
| 数値 | 0→9 |
| 英字 | A→Z |
| 日付 | 古→新 |
| かな | あ→ん |
| JISコード | 小→大 |
 バブルソート
バブルソート
・隣り合う要素の値を比較、大小が逆だったら交換、これを繰り返す方法
・整列のアルゴリズムの中でもっとも一般的
・通常は末尾からデータの検索を行う
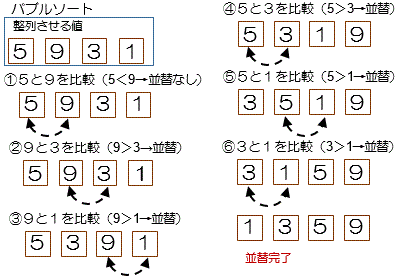
比較回数 並べ替える対象を n個としたとき、 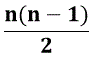 回 回 |
 選択ソート
選択ソート
・要素の列を端から順に比較、最小値を探す
・最小値を最初のデータと交換
・これを繰り返す
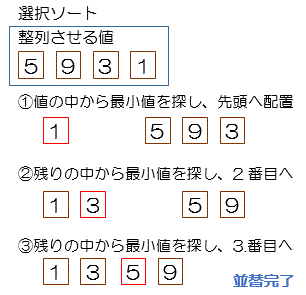
並べ替える対象をn個としたとき、 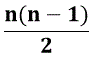 回 回 |
 挿入ソート
挿入ソート
・並んだ要素の最初の2つを比較、順に並べる
・3つ目の値を整列済みのデータと比較、挿入する
・これを繰り返す

並べ替える対象をn個としたとき、 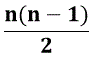 回 回 |
 シェルソート
シェルソート
・要素を一定間隔で挿入ソートを適用、大まかに整列
・次第にソートする間隔をつめていく
・最後に挿入ソートで整列
・挿入ソートの改良型
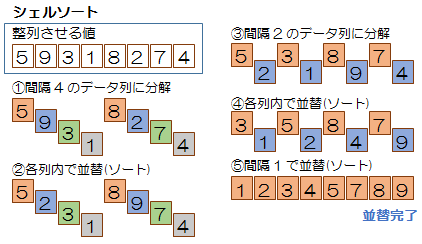
間隔の取り方によって整列の処理を行うための比較回数は異なる |
 マージソート
マージソート
・最初にデータ列を半分、またその半分と細かく分割
データ数が同じ列同士を整列、併合
・これを繰り返し、大きな列に併合する
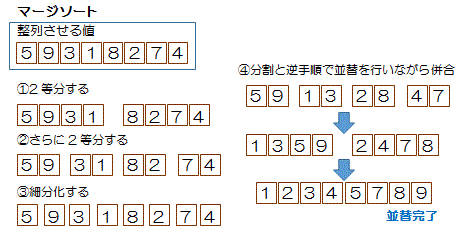
並べ替える対象をn個としたとき、 nlog2n回 |
 クイックソート
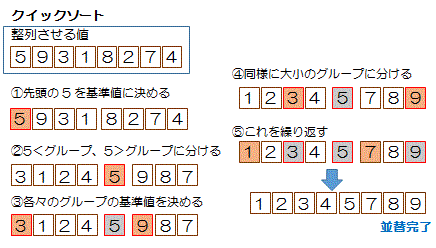
クイックソート
・基準値を決める
・基準値より小さいグループと、基準値より大きいグループに分ける
・できたグループ内でさらに同じ処理を繰り返していく
並べ替える対象をn個としたとき、 nlog2n回 |
 ヒープソート
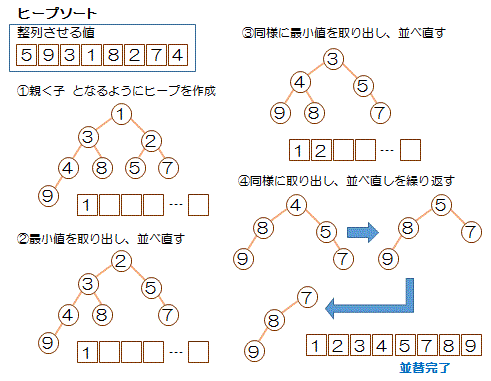
ヒープソート
・根が最大値(最小値)であるというヒープ構造を利用
・ヒープを構築
・根にあたるデータを取り出す
・残りの要素でヒープを再構築
・根にあたるデータを取り出す
・これを繰り返す
並べ替える対象をn個としたとき、 nlog2n回 |
再帰のアルゴリズム
定義の中に定義自身や簡略化した定義を使うこと
関数Aは自分自身である関数Aを使って計算するとき、関数Aは「再帰関数」という
再帰を使うメリット
●処理手順が短くなる
●プログラムがシンプルになる
| (例)整数nの階乗は以下のように再帰的に定義される (a)0!=1 (b)a>0ならばn!=n×(n-1)! |
 分割統治法
分割統治法
大規模な問題を効率的に解くアルゴリズムのひとつで、そのままでは解決することが難しい大きな問題を、いくつかの小さな問題に分割して個別に解決していくことで、最終的に大きな問題を解決する方式
 グラフのアルゴリズム
グラフのアルゴリズム
木構造やグラフを利用して、データを検索するためのアルゴリズム
●深さ優先探索
●幅優先探索
●最短経路探索 などがある
※木構造 木の巡回法 を参照
文字列処理のアルゴリズム
配列に格納されている文字列から、特定の文字列を検索するアルゴリズムのこと
 順次探索法
順次探索法
配列の先頭からひとつずつ文字列を照合して検索する

 ボイヤ・ムーア法
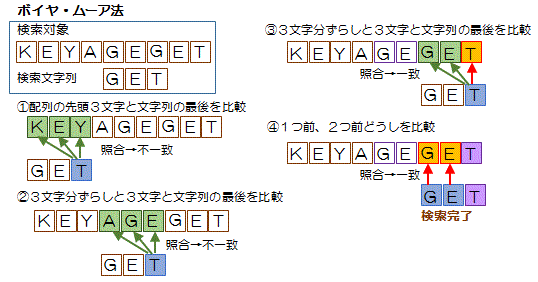
ボイヤ・ムーア法
配列は先頭から、文字列は最後尾から検索していく方法
一致すれば、順に前方に照合位置をずらし検索
文字列末尾の文字が文字列数の配列に現れない場合, 照合位置を文字列長飛ばす
文字列と配列の一致文字を そろえて,再照合を末尾から行う
ファイル処理のアルゴリズム
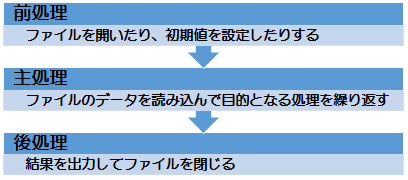
ファイルを読み込んで処理するアルゴリズム
基本的な手順は以下の通り
 コントロールブレーク処理(グループ集計処理)
コントロールブレーク処理(グループ集計処理)
基準となる項目ごとに整列されたファイルデータを集計する処理のこと
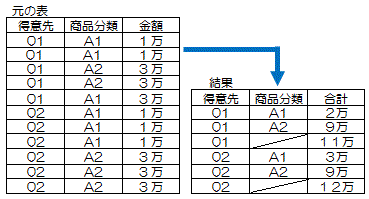
ファイルの併合・更新・照会 など
 併合処理
併合処理
あらかじめキー項目で整列されている2つのファイルを1つにまとめて、新しくファイルを作成すること

 ファイルの照会
ファイルの照会
マスタファイルのレコードをトランザクションファイルのレコードで参照すること
 ファイルの更新
ファイルの更新
マスタファイルのレコードをトランザクションファイルのレコードでマスタファイルのあるフィールドを更新すること
 整列処理
整列処理
ファイルのデータを基準となる項目で並べかえる処理のこと
 編集処理
編集処理
ファイルのデータを修正する処理のこと
アルゴリズムの評価
よいアルゴリズムとは
●処理が単純である
●使用するメモリの容量が少ない
●実行速度が速い
 オーダ記法
オーダ記法
実行にかかる時間の目安を「時間計算量」という尺度を用いてアルゴリズムを評価する。時間計算量は「Ο(オーダ)」という記号を使って表す。この方法を「オーダ記法」という
| アルゴリズム | オーダ記法 | |
|---|---|---|
| 探索 | 線形探索法 | Ο(n) |
| 2分探索法 | Ο(logn) | |
| ハッシュ法探索法 | Ο(1) | |
| 整列 | バブルソート | Ο(n2) |
| 選択ソート | Ο(n2) | |
| 挿入ソート | Ο(n2) | |
| マージソート | Ο(nlogn) | |
| クイックソート | Ο(nlogn) | |
| ヒープソート | Ο(nlogn) | |

