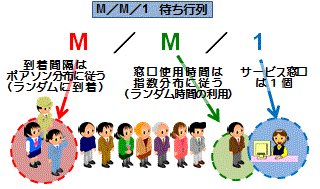
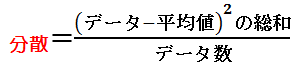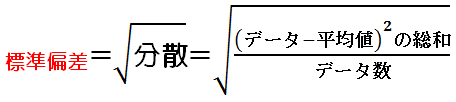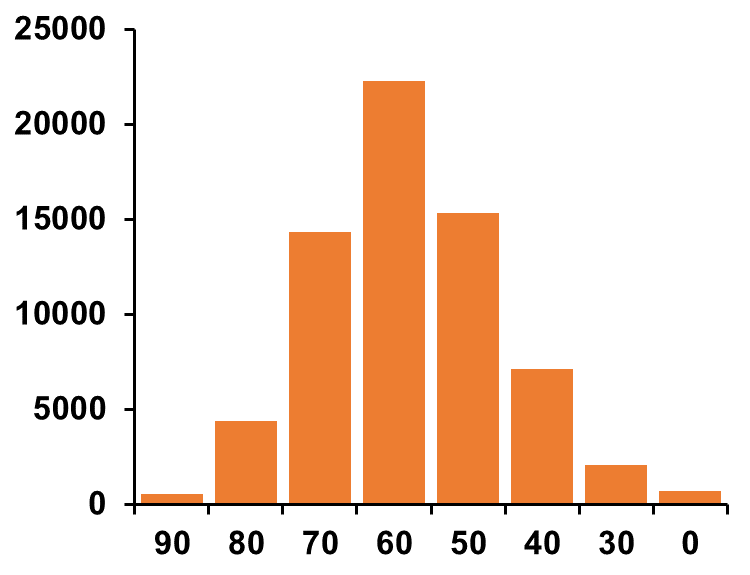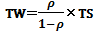基礎理論(2)
基礎理論
応用数学
収集したデータを分析し、数学的な知識を他の分野に適用することを目的とした数学
確率的手法
収集したデータがどの程度正確かを判断するために使用
場合の数
ある事象(出来事)が起こる可能性の総数のこと
| 名 称 | 説 明 | 法 則 |
|---|---|---|
| 和の法則 | 2つの事象A、Bが同時に起こらないことを前提とした場合、 事象Aの起こる場合がm通り、事象Bが起こる場合がn通りのときに、 事象A、Bが起こる場合の数の総数 | m+n通り |
| 積の法則 | 2つの事象A、Bが同時に起こることを前提とした場合、 事象Aの起こる場合がm通り、事象Bが起こる場合がn通りのときに、 事象A、Bが起こる場合の数の総数 | m×n通り |
順列
あるデータの集まりの中から任意の個数を取り出して並べる方法の総数のこと
| 異なるn個から任意にr個取り出して、1列に並べた順列の数を nPr と表した場合 |
組合せ
あるデータの集まりの中から任意の個数を取り出す方法の総数のこと
異なるn個から任意にr個取り出す組合せの数を nCr と表した場合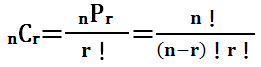 |
確率
すべての事象の数に対する、ある事象の起こりうる数の割合
 事象Aが起こる確率
事象Aが起こる確率
すべての事象の数がn通りで事象Aがそのうちr通り起こる確率P(A)は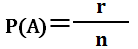 |
 事象Aが起こらない確率
事象Aが起こらない確率
| 事象Aが起こる確率P(A)とした場合、事象Aが起こらない確率P(A)は |
確率の基本定理
| 名 称 | 説 明 |
|---|---|
| 加法定理 | ・2つの事象A、Bが排反でない場合、事象AまたはBが起こる確率 P(AまたはB)=P(A)+P(B)−P(AかつB) ・2つの事象A、Bが排反である場合、事象AまたはBが起こる確率 P(AまたはB)=P(A)+P(B) |
| 乗法定理 | ・2つの事象A、Bが独立である場合、事象AかつBが同時に起こる確率 P(AかつB)=P(A)×P(B) ・事象Aが起こったという条件下で事象Bが起こる確率(条件付き確率) 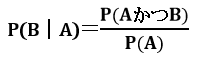 |
排反:2つの事象A、Bが決して同時に起こらないこと
独立:2つの事象A、Bが関係なく、同時に起こったり起こらなかったりすること
マルコフ課程
ある事象が起こる確率が過去の状態に関係なく、現在の状態だけに影響を受ける場合の課程のこと。「ひとつ前の状態にのみ依存する条件付き確率」
特にひとつの状態だけの影響を受ける場合を「単純マルコフ課程」という
≪情報処理試験でよく出る問題≫
表は、ある地方の天気の移り変わりを示したものである。例えば、晴れの翌日の天気は、40%の確率で晴れ、40%の確率で曇り、20%の確率で雨であることを表している。天気の移り変わりが単純マルコフ課程であると考えたとき、雨の2日後が晴れである確率は何%であるか。
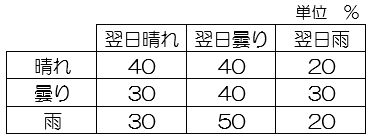 雨→晴れ→晴れ 0.3×0.4=0.12
雨→晴れ→晴れ 0.3×0.4=0.12
雨→曇り→晴れ 0.5×0.3=0.15
雨→雨→晴れ 0.2×0.3=0.06
雨の2日後が晴れとなる確率は、これらの和
ゆえに 0.12+0.15+0.06=0.33
確率分布
事象が起こる確率が変数によって決まる場合、変数と各事象が起こる確率との関係のこと
この変数を「確率変数」という
 正規分布
正規分布
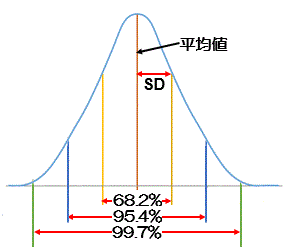
データの分析状態をグラフで表したときに、グラフの形が「正規曲線」になる分布のこと
【特徴】
●平均を中心とした左右対称のつりがね型
●平均±SD、±2SD、±3SDの確率がそれぞれ68.2%、95.4%、99.7%
 ポアソン分布
ポアソン分布
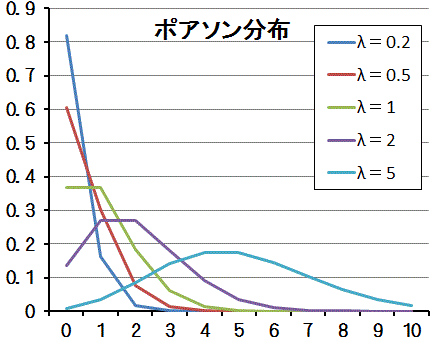
一定時間内にごくまれに起こる事象の確率分布のこと
「起こる確率が小さい」事柄が「n回起こる確率」を、横軸に回数n、縦軸にn回起きる確率でグラフにした分布
 指数分布
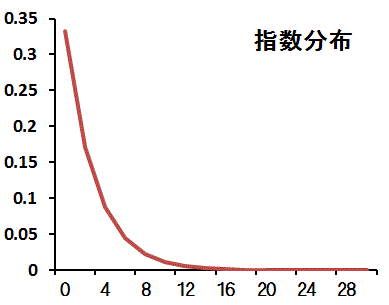
指数分布
一定時間内に起こる事象の時間間隔分布
統計
収集したデータの規則性を調べたり、予測したりするための手法
データの代表値
データ全体の特徴をひとつの数値で表現するもの
| 値 | 説明 |
|---|---|
| 平均値 | 全体の合計をデータ数で割った値のこと。一般的に"平均値"と呼んでいるものは、"算術平均"のこと |
| メジアン(中央値) | データを昇順、または降順に並べたときに中央に位置する値のこと。データが偶数の場合、中央に位置する2つの値の平均を使う |
| モード(最頻値) | データの出現度数の最も高い値のこと |
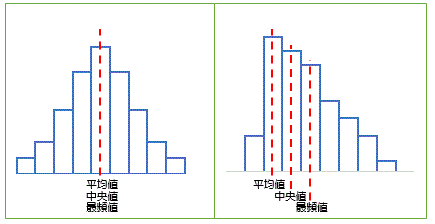 |
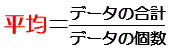 モード(最頻値):出現回数の一番多い値 メジアン(中央値):上から数えても、下から数えても真ん中の値 |
データの散布度
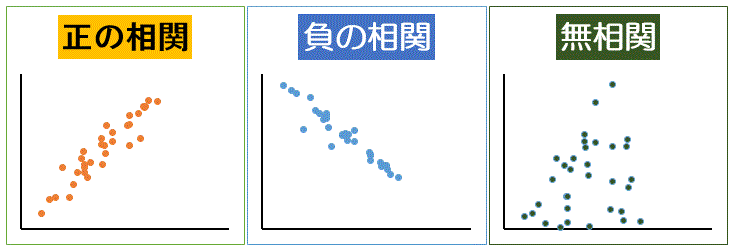
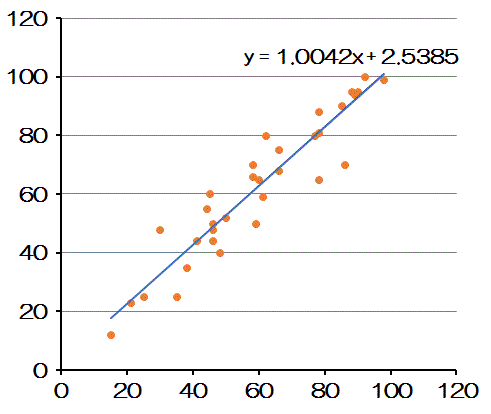
個々のデータが平均値を中心に周囲の値がどのようにばらついているかの度合いを示す数値を表現する。同じ平均値を持つデータの集まりでも上のグラフのように特徴が異なる場合がある。この違い(変量がどのように散らばっているか)を表現する数値。各変量の平均からの隔たりが大きいか小さいかを調べる「分散」「標準偏差」変量の分布の幅、散らばり具合の幅が大きいか、小さいかを示す「レンジ」がある
| 値 | 説明 | 計算式 |
|---|---|---|
| 分散 | 標本が標本平均からどれだけ散らばっているか | ([個々のデータの値]−平均)を2乗した値の平均 |
| 標準偏差 | 統計値や確率変数の散らばり具合(ばらつき)を表す数値 | 分散の平方根を取ったもの |
| レンジ(範囲) | 変動・影響などの範囲。分布幅を示す数値 | データの最大値と最小値の差 |