基礎理論(4)

アルゴリズムとプログラミング

データ構造

コンピュータの記憶装置内部でデータを系統立てて扱う仕組みのこと。データ構造の設計は全ての基礎となる

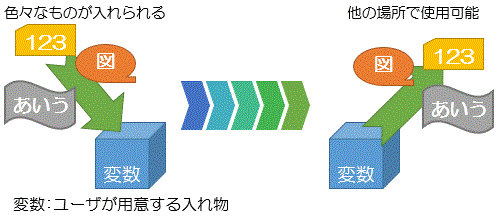
変数

プログラムの中で扱うデータを一時的に記憶し、必要なときに利用できるようにするために、データに固有の名前を与えたもの
●変数を定義する時は「a」や「b」などの変数名を付け、他のデータと区別する
●変数を使う時は、変数に値を代入する
●プログラムを実行するたびに異なる値を代入可能
●プログラム自体を書き換える必要がない
●ひとつのデータしか格納できない

フィールドタイプ(データ型)
変数に格納するデータの種類のこと。プログラムの中で扱うデータには、数値や文字列などのフィールドのタイプを定義する。そうすることによって適切なデータだけを代入できるため、プログラムの精度が向上する

名称	扱うデータ
数値型	整数値/td>
実数型	浮動小数点数、固定小数点数
論理型	真理値(True、False)
文字型	文字、文字列
抽象データ型	データとデータの操作をひとまとめにしたオブジェクト。ユーザ自身で定義可能
構造型	ひとつまたっは複数の値をひとつの構造としたもの。ユーザ独自で定義可能

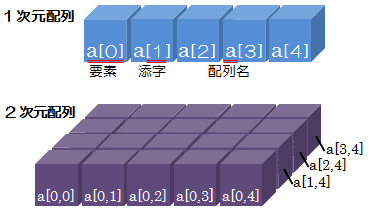
配列

●オブジェクトの並びのこと
●その要素(成分)が何番目か？というインデックス(添字)を用いて、どのデータにも
　直接アクセス可能(データを比較したり演算したりといった処理が簡単に行える)
●インデックスの範囲の範囲(配列の大きさ)に注意が必要
●複数のデータを格納できる
あらかじめ配列内の要素が決まっているものを「静的配列」、データの数によって配列内の要素の数が変化するものを「動的配列」という
横の一列に並んだデータのことを「1次元配列」横と縦の２つの例列に並んだデータのことを「2次元配列」という。2次元配列ではデータを呼び出すとき、縦横2つの添字で要素を指定する。

散在する複数のデータを数珠つなぎにするデータ構造。データとともに次のデータの格納場所を示す「ポインタ」と呼ばれる情報を持っているので、データが連続的に配置されていなくてもOK。実際には列で並んだデータが複数の列となり「ファイル」としてまとめられている。

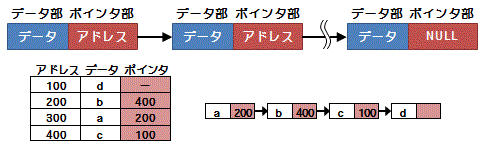
リストの特徴：
●サイズは固定ではなく、データの大きさに柔軟に対応可能
●ポインタの付け替えだけで並べ替えが可能
●データの挿入や削除を行っても、他のデータを動かす必要がない

リストの種類

名称	説明
線形リスト単方向リスト	一方方向にしかデータを呼び出すことが出来ないリスト。次のデータを呼び出すポインタのみを持っている
相方向リスト	次のデータだけでなく、前のデータも呼び出すことが出来るリスト。次のデータを呼び出す「次ポインタ」と麻円のデータを呼び出す「前ポインタ」を持っている
環状リスト	全てのポインタが環状につながっているリスト。最後のデータは最初のデータを呼び出すポインタを持っている

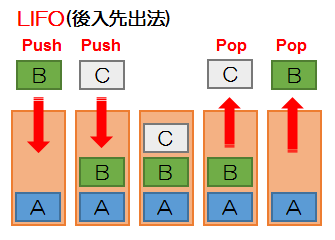
スタック

リストにデータの挿入や削除を行う考え方
後に入れたデータが先に取り出される
データを入れることをPush(プッシュ)、データを取り出すことをPop(ポップ)という

キュー

リストにデータの挿入や削除を行う考え方
先に入れたデータが先に取り出される
データを入れることをEnqueue(エンキュー)、データを取り出すことをDequeue(デキュー)という

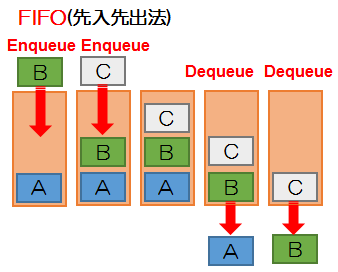
スタック：後入れ先出し
　　　　PUSH：データ挿入
　　　　POP：最後のデータ削除
キュー：先入れ先出し
　　　　ENQUEUE：データ挿入
　　　　DEQUEUE：最初のデータ削除

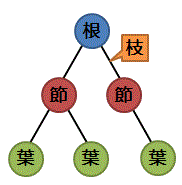
木構造

データを階層構造で管理するときに使われる図のこと
各要素を「節(ノード)」、最上位の節を「根(ルート)」、最下位の節を「葉(リーフ)」、各節を関連付ける線を「枝(ブランチ)」という

木の巡回法

木構造からデータを読み出すこと

幅優先探索

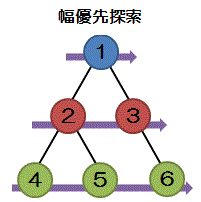
根を開始地点として同じレベルにある節や葉を左から右に巡回してデータを読み出す方法

レベル

木構造の階層の深さのこと

深さ優先探索

根から葉までの深さを探索したうえで、順に巡回してデータを読み出す方法
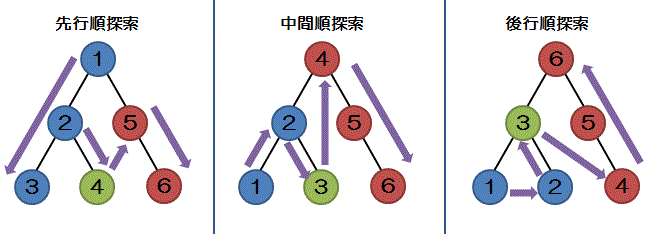
深さ優先探索は木を巡回する順番によって以下のように分類される

名称	説明
先行順探索	親、左部分木、右部分木の順にデータを読み出す
中間順探索	左部分木、親、右部分木の順にデータを読み出す
後行順探索	左部分木、右部分木、親の順にデータを読み出す

左部分木と右部分木

木の一部分を「部分木」といい、節の左側にある部分木を「左部分木」、右側を「右部分木」という

後行順探索と逆ポーランド表記法

後行順探索でデータを読み出すと逆ポーランド表記法に変更できる

2分木

節から分岐する枝が2本以下の構造のこと

完全2分木

■根からすべての深さが等しい2分木のこと
■根からすべての葉までの深さの差が1以下で、葉が左にひとつだけ配置されている2分木

多分木

節から分岐する枝が2つより多い木構造のこと

ヒープ

すべての節で親と子の間に以下のような一定の大小関係が成立する完全2分木のこと
親≧子　または　親≦子

根に最大値または最小値が格納されるので、根のデータを順番に取り出すことでデータの整列を行える
　(例)ヒープ(親≧子)を構築する
　　1.根から左の子、右の子の順番で比較する
　　2.親と左の子を比較して、「親≧子」でなければ入れ替える
　　3.親と右の子を比較して、「親≧子」でなければ入れ替える
　　4.1～3を繰り返す

順序木

節の順に順序性がある木構造のこと

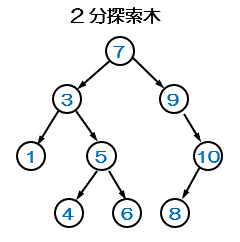
2分探索木

節のデータを昇順または降順に並べておくことで、効率的に探索できる2分木のこと。すべての節で「左部分木＜親＜右部分木」が成立するようにする

節の追加

「左部分木＜親＜右部分木」の規則に従って行う
追加する要素が根よりも小さければ左へ、大きければ
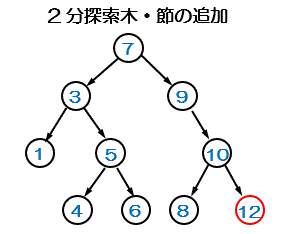2分探索木・追加右へ進む。この作業を繰り返し、追加すべき葉または節を探す。その葉(節)の左または右に新しい要素を追加する
　(例)上の木構造に節「12」を追加する
　　1.根の「7」と比較、7＜12なので、右部分木へ
　　2.「9」と比較、9＜12なので、右部分木へ
　　3.「10」と比較、10＜12なので、右の節に追加

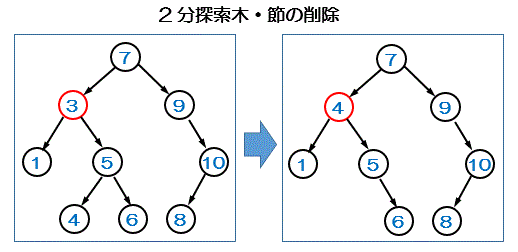
節の削除

「左部分木＜親＜右部分木」の規則に従って行う
■子がなければ(削除する節が葉であれば)、削除
■子が1つなら子を根のあった部分に移動
■子が2つなら削除する節の右部分木の中から、最も小さいデータを持つ節を、
　削除する節の部分に移動(あるいは、左部分木の中から最も大きいデータを
　持つ節を移動)
　(例)上の木構造の節「3」を削除する
　　1.バランスが良くなるように今回は右部分木から移動させる
　　2.「3」を削除
　　3.右部分木の最小値データ「4」を「3」の節の位置に移動

バランス木(平衡木)

データの挿入や削除を繰り返して、木の形が変形し、アンバランスな木の形になる。このようなアンバランスな状態を避ける仕組みを持った木で、根から子を持たない末端の葉までの高さ(深さ)がなるべく等しくなるように構築されたもの

名称	説明
AVL木	すべての節で、左部分木と右部分木のレベル差が1以下の2分木
B木	すべての節で、左部分木と右部分木のレベルが同じ多分木