アルゴリズムとプログラム(1)

データ構造

配列とリスト

複数のデータを効率よく処理するためのデータ構造

	配列	リスト
順序の示し方	添え字を利用	ポインタを利用
メモリへの格納方法	連続した領域に格納	順序は無関係で空き領域に格納
データアクセス	添え字によるランダムアクセスが可能	先頭から順にたどる必要がある
データの挿入	挿入位置により後ろのデータを後ろにずらしておく必要がある	ポインタの付け替えだけで可能
データの削除	削除したデータより後ろのデータを前に詰めておく必要がある	ポインタの付け替えだけで可能
メモリ使用量	小	大
データ数	あらかじめ決めておく	可変

スタックとキュー

リストにデータの挿入や削除を行う考え方

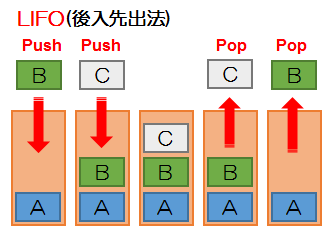
スタック

リストにデータの挿入や削除を行う考え方
後に入れたデータが先に取り出される
データを入れることをPush(プッシュ)、データを取り出すことをPop(ポップ)という

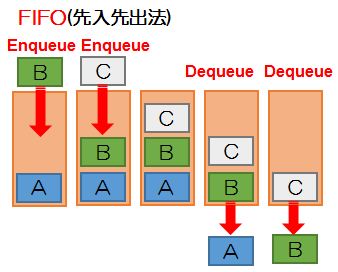
キュー

リストにデータの挿入や削除を行う考え方
先に入れたデータが先に取り出される
データを入れることをEnqueue(エンキュー)、データを取り出すことをDequeue(デキュー)という

スタック：後入れ先出し
　　　　PUSH：データ挿入
　　　　POP：最後のデータ削除
キュー：先入れ先出し
　　　　ENQUEUE：データ挿入
　　　　DEQUEUE：最初のデータ削除

木構造

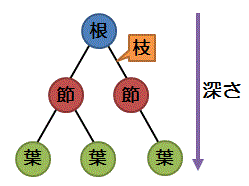
データを階層構造で管理するときに使用される図のこと
各要素を「節(ノード)」、最上位の節を「根(ルート)」、最下位の節を「葉(リーフ)」という。また各節を関連付ける線を「枝(ブランチ)」という。ルートからそのノードまでにたどる経路の長さを「深さ」という。また、木の中の一つのノードとその先にあるすべてのノードを「部分木」という

木の巡回法

木構造からデータを読み出すこと

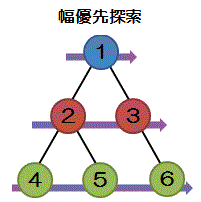
幅優先検索

根を開始地点として同じレベルにある節や葉を左から右に巡回してデータを読み出す方法

深さ優先検索

根から葉までの深さを探索したうえで、順に巡回してデータを読み出す方法
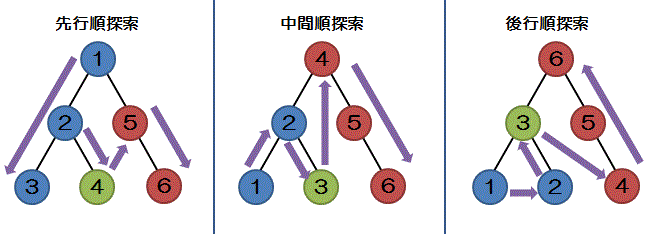
深さ優先探索は木を巡回する順番によって以下のように分類される

先行順探索	親、左部分木、右部分木の順にデータを読み出す
中間順探索	左部分木、親、右部分木の順にデータを読み出す
後行順探索	左部分木、右部分木、親の順にデータを読み出す

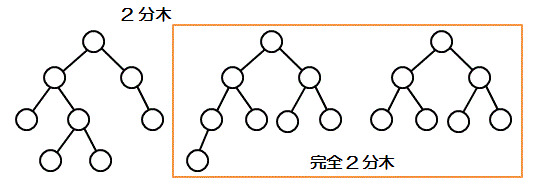
2分木

節から分岐する枝が2本以下の構造の木のこと

完全2分木

■根からすべての深さが等しい2分木のこと
■根からすべての葉までの深さの差が1以下で、葉が左にひとつだけ配置されている
　2分木

木の深さ＝n　の時
　　　同じ深さの節点の個数(葉の個数)　⇒2ⁿ
　　　節点の全個数　　　　　　　　　　⇒2ⁿ⁺¹－1
　　　枝の全個数　　　　　　　　　　　⇒節点の全個数－1＝2ⁿ⁺¹－2

多分木

節から分岐する枝が2つより多い木構造のこと

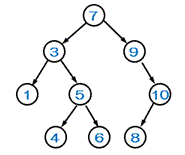
2分探索木

節のデータを昇順または降順に並べておくことで、効率的に探索できる2分木のこと。すべての節で「左部分木＜親＜右部分木」が成立するようにする

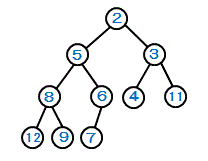
ヒープ

すべての節で親と子の間に親≧子　または　親≦子」が成立する完全2分木のこと

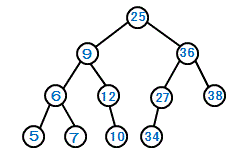
AVL木

どの節点においても、その「左部分木の高さ」と「右部分木の高さ」の差が1以下となる木のこと

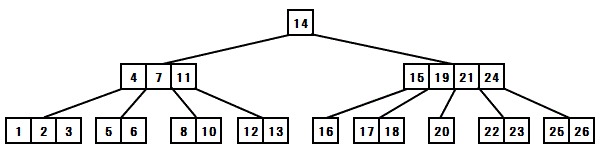
B木

すべての節で左部分木と右部分木のレベルが同じ多分木
多分岐の平衡木(バランス木)である。1 ノードから最大ｍ個の枝が出るとき、これをオーダーｍのB木という
　1.各ノードは最大でｍ本の枝を持つ(ｍ≧3)
　2.根以外の各ノードは、ｍ/2本の枝を持つ
　3.ノード内のキー値は常に昇順で整列されている
　4.ｍ個の枝を持つノードはｍ＋1個の子を持つ
　5.葉はすべて同じレベルになる
各ノードのつながりに、一定の大小関係をもって構成されている。ノード間に一定の大小関係があるおかげで、データ検索時に余計なノードにアクセスすることなく、確実にデータのあるノードに近づくことができる。2分探索木が、下に伸びるリンクが2つなのに対して、B木は下方へのリンク数を増やして、木の高さを抑え、データ探索時にアクセス回数を大幅に減らせるというメリットが生まれる