アルゴリズムとプログラム(2)
代表的アルゴリズム
整列(ソート)
複数のデータを昇順あるいは降順に並べ替える処理のこと
バブルソート
先頭または末尾からデータを検索し、隣接したデータの値を比較しながら整列するアルゴリズム。整列のアルゴリズムの中で、最も一般的な方法。通常は末尾からデータの検索を行う
選択ソート
先頭から順にデータ同士を比較することで最小値を検索し、発見した最小値を先頭のデータと差し替える処理を繰り返すことで、データを整列するアルゴリズム
挿入ソート
挿入するデータと整列済みのデータの2つを比較し、間sに挿入して並べるアルゴリズム
クイックソート
配列の中間に位置するデータを基準値として、基準値より左側に小さいデータ、基準値より大きいデータを配置し、これを繰り返して整列するアルゴリズム
比較回数はnlog2n、安定ソートではない
シェルソート
ある間隔だけ離れたデータを取り出して整列し、その間隔を徐々に狭くしていく方法。挿入ソートの改良版
比較回数は平均してn1.25程度、安定ソートではない
ヒープソート
木構造のヒープは根が最大値(or最小値)となっていることから、ヒープの根にあたるデータを取り出すことで整列が可能。これを利用したアルゴリズム。選択法の改良版
1.ヒープを構築する
2.根にあたるデータを取り出す
3.ヒープを再構築する
4.根にあたるデータを取り出す
比較回数はnlog2n、安定ソートではない
マージソート
配列を2等分し、2等分した配列内で整列されていれば2つの配列を併合するアルゴリズム。2等分した配列内で整列されていない場合は、さらにその配列を2等分する比較回数はnlog2n、安定ソート
| 名称 | 平均計算時間 | 最悪計算時間 | 安定性 | 備考 |
|---|---|---|---|---|
| バブルソート | − | n2 | 〇 | 安定ソートとしても実装可能 |
| 選択ソート | n2 | n2 | × | |
| 挿入ソート | n+d | n2 | 〇 | dは置換群の反転数で、Ο(n2) |
| クイックソート | nlog2n | n2 | × | ピボット値として中央値を使えば、 最悪時間がΟ(nlog2n) |
| シェルソート | n1.25程度 | nlog2n | × | |
| ヒープソート | nlog2n | nlog2n | × | |
| マージソート | nlog2n | nlog2n | 〇 |
検索
配列に格納されているデータを探す処理のこと
線形探索法(リニアサーチ)
配列に格納されているデータを先頭から末尾まで順番に探していくアルゴリズム
 番兵法
番兵法
線形探索法は配列内に目的データが存在することを前提とした場合にのみ成立する。配列内に目的データが存在しない場合を想定し、探索前に目的データを配列の最後に追加しておくこと
2分探索法(バイナリサーチ)
対象が、データ群の中央にあるデータより前にあるか、後ろにあるかを判断し、2分したデータ群を取捨選択する。これを繰り返して絞り込んでいくアルゴリズム。データを昇順に整列させておく必要がある
| 要素数n | 最短 | 最大 | 平均 |
|---|---|---|---|
| 線形探索法 | 1回 | n回 | n/2回 |
| 2分探索法 | 1回 | log2n+1回 | log2n回 |
| ●log2nの計算の仕方 log2n=log10n/log102 (log102=0.301) |
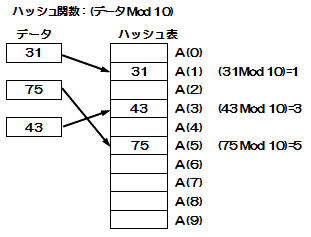
ハッシュ表探索法
データを格納するときにあらかじめ関数を使ってデータの格納位置を決め、データを探し出すときに同じ関数を使って格納位置を算出するアルゴリズム
ハッシュ値(ハッシュキー):データの格納位置
ハッシュ関数:ハッシュキーを決めたり探し出したりする関数
ハッシュ表データを格納した表
 ハッシュ表におけるシノニム
ハッシュ表におけるシノニム
ハッシュ表探索法では、ハッシュキーが同じ場合、ハッシュ表にデータを格納する際にデータ同士の衝突が発生する。このデータの衝突を「シノニム」という
モンテカルロ法
反復計算と乱数を用いて、数値実験によって問題の近似解を求めるシミュレーション技法
再帰
再帰呼び出し
定義の中に定義自身や簡略化した定義を使うこと
例えば、関数Aは自分自身である関数Aを使って計算するとき、関数Aは「再帰関数」という
 メリット
メリット
●処理手順が短くなる
●プログラムがシンプルになる
 注意点
注意点
●どこかで再帰呼び出しを止める形にする必要がある
●再帰関数を計算するときは途中の経過を保存するためにLIFOのスタック領域を
使用する。
場合によってはスタック領域が不足するスタックオーバーフロー
状態を引き起こすことがある
※注意※
再帰関数を使用すると再帰関数部分で入れ子状態となる
その他
分割統治法
大規模な問題を効率的に解くアルゴリズムの一つで、そのままでは解決することが難しい大きな問題を、いくつかの小さな問題に分割して個別に解決していくことで、最終的に大きな問題を解決する方式
クイックソート、マージソートなどの並べ替えアルゴリズムでよく用いられ、効率よく階乗を求めるアルゴリズムなどでも使われている。アルゴリズムの中に取り入れて実装するには、「再帰呼び出し」という方法が使われることが多い。大きな問題を部分に分割する論理を簡潔に記述することができる反面、現在の状態を保持しておく必要があるためメモリを大量に消費し、プログラムの実行速度が低下する可能性がある
オブジェクト指向
ソフトウェアの設計や開発において、操作手順よりも操作対象に重点を置く考え方。関連するデータの集合と、それに対する手続き(メソッド)を「オブジェクト」と呼ばれる一つのまとまりとして管理し、その組み合わせによってソフトウェアを構築する。データと手続きを一体化したオブジェクトによってモデル化する考え方
動的計画法
問題の部分的最適解を求め、それを拡張して全体解を求める手法

