基礎理論(1)
離散数学
基数変換
ある進数から別の進数に置き換えること
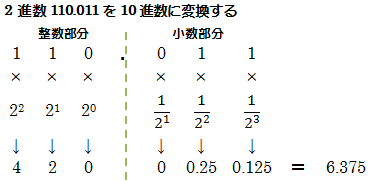
2進数→10進数
桁の重みに桁に書かれた数値をかけ、その結果をすべて加算する (下図参考)
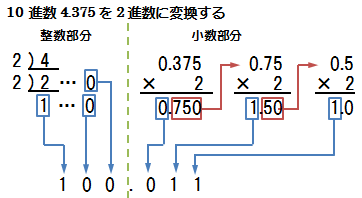
10進数→2進数
| 整数部: | 10進数を2で割って商と余りを求め、商が1になるまで繰り返し、 |
| 求めた余りを下位桁から並べる (下図参考) | |
| 小数部: | 10進数に2をかけて、小数部が0になるまで繰り返し、求めた結果の |
| 整数部を上から順番で記述する (下図参考) |
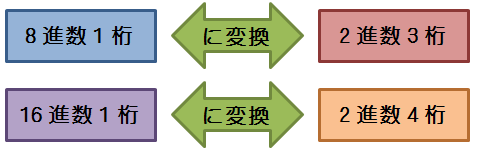
2進数→8進数・16進数
小数点を基点にして、8進数であれば3桁ごと、16進数であれば4桁ごとに区切る
整数部は右→左に、小数部は左→右に区切り、それぞれを8進数or16進数に変換
※3桁(8進数)、4桁(16進数)にならない場合は、不足している桁数ぶん0を補充する
8進数・16進数→2進数
1桁ずつ2進数に変換し、記述する
| 2進数→8進数 :3桁に区切って、2進数の桁の重みを掛けて足す 2進数→16進数:4桁に区切って、2進数の桁の重みを掛けて足す n進数→10進数:n進数の各桁の数値と桁の重みを掛けて足す (整数部、小数部共に) 10進数→n進数:10進数をnで割り、余りを下位桁から並べる(整数部) :10進数にnを掛けて小数部が0になるまで繰り返し、整数部を 上から記述(小数部) |
 無限小数
無限小数
10進数の小数部を2進数に変換時、2を掛けた演算結果の小数部が0にならない小数。
(例:(0.1)10=(0.00011001100…)2 故に(0.1)10は無限小数)
見分け方:先ず分数にして、2の累乗のみの数字で構成されていたら有限小数
シフト演算
ビットの位置を左や右にずらすことで、数値の乗・除算を高速に処理する方法
| ●左にずらす(左シフト):元の数値の2のn乗倍(2のn乗で乗算) ●右にずらす(右シフト):元の数値の2の-n乗倍(2のn乗で除算) |
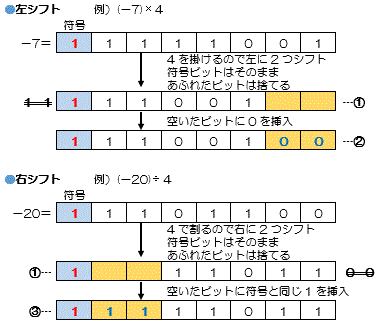
算術シフト
正負を考慮した数値演算を行う時に使用
a)符号ビットを除くビット列をシフトする ---①
b)はみ出したビットは切り捨てる ---①
c)空いたビット位置には
左シフト:"0" ---②
右シフト:符号ビットと同じ値 ---③
を格納する
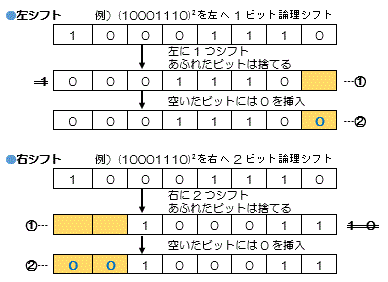
論理シフト
数値演算ではなく、単にビットの位置を移動するときに使用
a)符号ビットを含むすべてのビット列をシフトする ---①
b)はみ出したビットは切り捨てる ---①
c)空いたビット位置には"0"を格納する ---②
負の整数と補数
| 1の補数表現:各桁の1と0を反転する 2の補数表現:各桁の1と0を反転+1 |
小数の表現
浮動小数点数
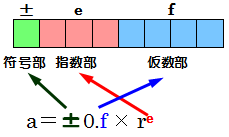
小数点の位置を移動し、より詳細な数値を実現する方法
一般的にコンピュータなどは、整数部と小数部を分けて数値管理を行い、小数部のデータ表現において浮動小数点数を用いている
浮動小数点数では、実数aを「a=0.f×re」(f=仮数、e=指数、r=基数)という形で表現する
| 名称 | 説明 |
|---|---|
| 符号部 | 数値が正か負かを表す。正の場合0、負の場合1 |
| 指数部 | 基数のべき乗を2進数で表す。負のべき乗は2の補数を使用 |
| 仮数部 | 小数点以下の数値を表す。正規化しておく |
誤差
コンピュータ上で数値表現に使用できるビット数が決まっているため、演算結果に実際の数値とコンピュータで表現する数値の差「誤差」が生じる
丸め誤差
小数点以下の極めて小さい単位で値を丸めて計算した結果、計算結果と正しい値がわずかにずれること
最下位桁より小さい部分を四捨五入や切捨て、切り上げを行うときに生じる誤差
けた落ち
浮動小数点演算で、計算結果が0に極端に近くなる加減算を行ったときに、有効数字の桁数が極端に少なくなること
(例:「0.123456x102-0.123455x102」のような計算を行うと、「1x10-4」となり、有効数字の桁数は7桁から一気に1桁に減少してしまう)
浮動小数点形式では常に有効数字の桁数を一定にして扱っているため、けた落ち時に不足した桁数を自動的に0で埋めてしまい、真の値との間に誤差が発生してしまう。その値を計算に使用することで大きな誤差を含んだ値が返されることがある
情報落ち
絶対値の大きさが極端に異なる数字の加・減算時に小さい値の情報が無視されること。そのことによって起きる計算の誤差
大きさが極端に異なる値を多数計算する場合、情報落ちの影響で適切な計算結果が得られないことがあるため、工夫必要となる
オーバーフロー(桁あふれ)
数値演算を行った結果の絶対値が、扱える数値の最大値を超えること
一つの数値を表現するために割り当てられた記憶容量の上限を超えた状態
| -2(n-1)<=和 AND 和<2(n-1) |
アンダーフロー
浮動小数点演算処理で、計算結果の指数部分が小さくなり過ぎ、使用している記述方法では数値が表示できなくなる状態

論理演算
論理演算:複数の条件(論理)の組み合わせを条件式で表した時の演算方法
論理回路:コンピュータ内部の論理演算を担当する電子回路
「回路記号(MIL記号)」を使って図で表現する
論理記号
論理演算を行うときに使われる記号
| 名称 | 説明 | 回路記号 | 論理記号 | 例 |
|---|---|---|---|---|
| 論理積(AND) | 2つの入力値がともに1のとき1、 それ以外は0を出力 |  | ・ , ∧ | X・Y X∧Y |
| 論理和(OR) | 2つの入力値がともに0のとき0、 それ以外は1を出力 |  | + , ∨ | X+Y X∨Y |
| 否定(NOT) | 入力値が1ならば0、 0ならば1を出力 | 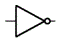 | ― , ¬ | X ¬X |
| 否定論理積 (NAND) | 論理積と否定を組み合わせた論理演算 2つの入力値がともに1のとき0、 それ以外は1を出力 | 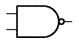 | ||
| 否定論理和 (NOR) | 論理和と否定を組合わせた論理演算 2つの入力値がともに0のとき1、 それ以外は0を出力 | 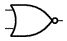 | ||
| 排他的論理和 (EOR , XOR) | 論理積tと論理和と否定を組合わせた論理演算 2つの入力値が同じなら0、 異なるなら1を出力 | 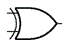 | X X∀Y |
真理値表
| 論理積 | 論理和 | 否定 | 否定論理積 | 否定論理和 | 排他的論理和 | ||
|---|---|---|---|---|---|---|---|
| AND | OR | NOT | NAND | NOR | EOR , XOR | ||
| X | Y | X・Y | X+Y | X | X・Y | X+Y | X∀Y |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
※排他的論理和演算の結果:
演算対象ビットの“1”の数が奇数→1
偶数→2
論理演算の法則
| べき等則 | A+A=A A・A=A |
|---|---|
| 交換則 | A+B=B+A A・B=B・A |
| 分配則 | A・(B+C)=(A・B)+(A・C) A+(B・C)=(A+B)・(A+C) |
| 結合則 | (A+B)+C=A+(B+C) (A・B)・C=A・(B・C) |
| 吸収則 | A+(A・B)=A A・(A+B)=A |
| 復元則 | |
| ド・モルガンの法則 | A+B=A・B A・B=A+B |
| 論理積の法則 | A・A=0 A・0=0 A・1=A |
| 論理和の法則 | A+A=1 A+0=A A+1=1 |
半加算器と全加算器
四則演算や論理演算を行う回路を「演算回路」といい、2進数の加算を行う演算器を「加算器」という
加算器には「半加算器」と「全加算器」がある
半加算器
2進数の加算で下位の桁から桁上がりを考慮しない加算器のこと
論理積と排他的論理和の回路の組合せで構成される
【特徴】
●2進数の加算を行うための、最下位ビットの加算
●半加算器は2ビット以上の桁をもつ加算には使用不可
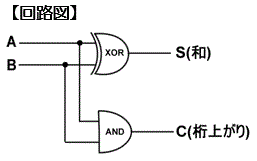
| 入 力 | 出 力 | ||
|---|---|---|---|
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
全加算器
2進数の加算で下位の桁からの桁上がりを含める加算器のこと
2個の半加算器と論理和の回路の組合せで構成される
【特徴】
●下位の桁からの桁上がりを含む加算
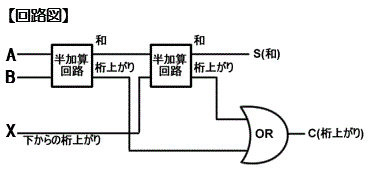
| 入 力 | 出 力 | |||
|---|---|---|---|---|
| A | B | X | C | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
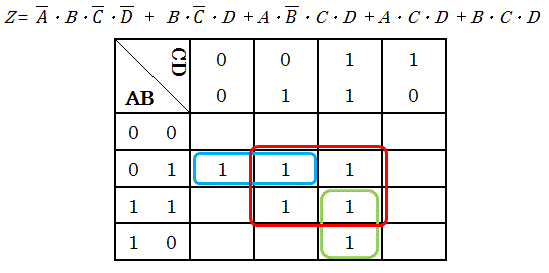
カルノー図
1.論理式の値が1のとき1を記入
2.1のセルを出来るだけ少ない長方形で囲む(共有はOK)
3.共通変数を取り出しかける(積)をつくりそれを足算する(0はA)