基礎理論(2)
応用数学
順列・組合せ
場合の数
ある事象(出来事)が起こる総数のこと
| 名称 | 説明 | 法則 |
|---|---|---|
| 和の法則 | 2つの事象A、Bが同時には起こらないことを前提として、Aの起こ場合がm通り、Bの起こる場合がn通りのときに、A、Bのどちらかが起こる場合の数の総数 | m+n 通り |
| 積の法則 | 2つの事象A、Bが同時に起こることを前提として、Aの起こ場合がm通り、Bの起こる場合がn通りのときに、A、Bが同時に起こる場合の数の総数 | m×n 通り |
順列
あるデータの集まりの中から任意の個数を取り出して並べる方法の総数のこと
| 異なるn個から任意にr個取り出して、1列に並べた順列の数を nPr と表した場合 |
組合せ
あるデータの集まりの中から任意の個数を取り出す方法の総数のこと
異なるn個から任意にr個取り出す組合せの数を nCr と表した場合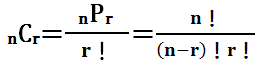 |
確率
すべての事象の数に対する、ある事象の起こりうる数の割合
 事象Aが起こる確率
事象Aが起こる確率
すべての事象の数がn通りで事象Aがそのうちr通り起こる確率P(A)は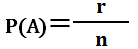 |
 事象Aが起こらない確率
事象Aが起こらない確率
| 事象Aが起こる確率P(A)とした場合、事象Aが起こらない確率P(A)は |
確率の基本定理
| 加法定理 | ・2つの事象A、Bが排反でない場合、事象AまたはBが起こる確率 P(AまたはB)=P(A)+P(B)−P(AかつB) ・2つの事象A、Bが排反である場合、事象AまたはBが起こる確率 P(AまたはB)=P(A)+P(B) |
|---|---|
| 乗法定理 | ・2つの事象A、Bが独立である場合、事象AかつBが同時に起こる確率 P(AかつB)=P(A)×P(B) ・事象Aが起こったという条件下で事象Bが起こる確率(条件付き確率) 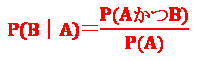 |
排反:2つの事象A、Bが決して同時に起こらないこと
独立:2つの事象A、Bが関係なく、同時に起こったり起こらなかったりすること
マルコフ課程
ある事象が起こる確率が過去の状態に関係なく、現在の状態だけに影響を受ける場合の課程のこと。「ひとつ前の状態にのみ依存する条件付き確率」
特にひとつの状態だけの影響を受ける場合を「単純マルコフ課程」という
≪情報処理試験でよく出る問題≫
表は、ある地方の天気の移り変わりを示したものである。例えば、晴れの翌日の天気は、40%の確率で晴れ、40%の確率で曇り、20%の確率で雨であることを表している。天気の移り変わりが単純マルコフ課程であると考えたとき、雨の2日後が晴れである確率は何%であるか。
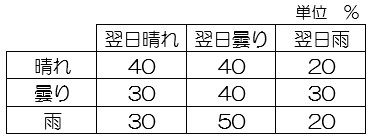 雨→晴れ→晴れ 0.3×0.4=0.12
雨→晴れ→晴れ 0.3×0.4=0.12
雨→曇り→晴れ 0.5×0.3=0.15
雨→雨→晴れ 0.2×0.3=0.06
雨の2日後が晴れとなる確率は、これらの和
ゆえに 0.12+0.15+0.06=0.33
数値計算
行列
数値や文字列を下図のように長方形に並べたもの
横方向に並んでいる数値や文字列の並びを「行」、縦方向を「列」と呼び、並べる数はいくつでも構わない
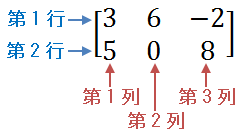
 行列の性質
行列の性質

対数
乗算や除算を加算や減算で行うことが出来る数値計算方法のひとつ。対数を使用することで計算を簡略化できるというメリットがある
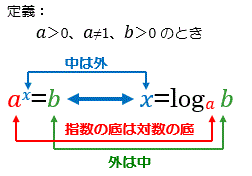
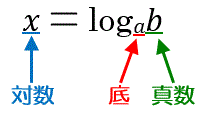
 対数の性質
対数の性質

統計

 相関係数
相関係数
バラツキを表す
 回帰直線
回帰直線
2変数の相関関係を表す近似直線

