基本理論(1)
基本理論
離散数学
数と表現
自然界において、物理的な重さや長さ、時間といった指針による、連続した値は「アナログ」と呼ぶ。これに対して、個数をはじめとした離散的な量による表現は「デジタル」と呼ぶ
コンピュータは、ある=1、ない=0、といったように、1と0によって値を表現する2進数デジタルの処理を得意としています。2進数で表現される1桁の値は「ビット(bit)」と呼ばれる(ビットは「binary digit」の略)
数字やアルファベットなどの文字情報を表現するためには、2の8乗=256通りとなる8ビットでひとつの文字を作る。この8ビットは「バイト(byte)」という単位でまとめて扱われる。日本語の場合、カナや漢字など多数の文字が用いられるため、1バイトで表現しきることができません。そのため、通常はカナや漢字は2バイトで表現される。2バイト使用すると2の16乗=65536通りの文字を表現できる
ビットとバイトは、アルファベット表示だと両方「b」が頭文字となるが、通例として、ビットを小文字の「b」、バイトを大文字の「B」で書き分け、それぞれ略号としている
2進数・8進数・10進数・16進数
 2進数
2進数
数値の表現形式のうち、「0」と「1」の2種類の数字の組み合わせによって数値を表現する形式のこと
2進数は、1つの桁を0と1のみで表現できるため、電子回路などにおけるスイッチの入切、プラスマイナスの反転などによって数値表現を行うことができる。このため、コンピュータの内部におけるあらゆるデータは2進数の値として処理されている
2進数では、2を基数とし、2倍ごとに位取りを行う。0と1の次は位取りして「10」となり、その次は「11」、その次はまた位取りして「100」となる。基数が小さいため、非常に多くの場合、数値を表現するために膨大な桁数を必要とする
コンピュータ上で数値を扱う形式としては、2進数の他に、8進数や16進数などもある。2進数は処理上の都合はよいが、表現する上で桁数が非常に多くなるという難点があるため、2進数における3桁をまとめて8進数で表したり、2進数における4桁をまとめて16進数で表したりするといった表現をとる場合もある
| 2進数⇔10進数⇔18進数⇔16進数 | 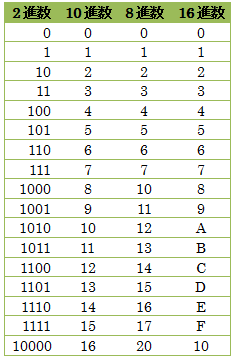 |
 10進数
10進数
数値の表現形式のうち、「0」から「9」までの10種類の数字を使って数値を表現する形式のこと
 8進数
8進数
数値の表現形式のうち、「0」から「7」までの8種類の数字を使って数値を表現する形式のこと。8進数は、16ビットのコンピュータなどでよく用いられていた。今日では、同様の目的で16進数が多く採用されている
 16進数
16進数
0から9までの10個の数字と、AからFまでの6個のアルファベットを使って数値を表現する方法。日常生活においては、0から9までの10個の数字を使った10進数が主に使われているが、コンピュータでは2進数などと並んで16進数を扱うことも多い。例えばASCIIコードや日本語の文字コード、色を示すカラーコードなどは16進数を使用している
基数変換
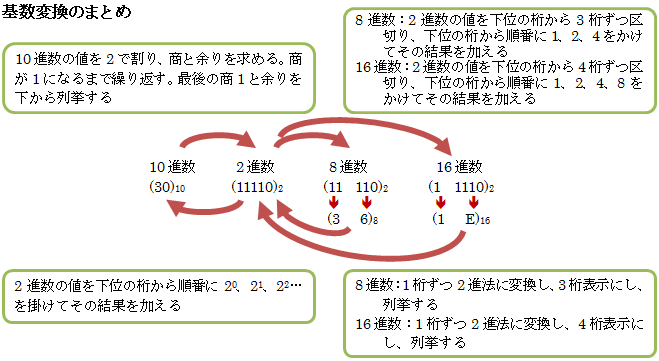
ある進数から別の進数へと変換する作業は「基数変換」と呼ばれる
 10進数を2進数に変換する
10進数を2進数に変換する
変換したい10進数を商が1になるまで2で割りつづけ、最後の商1と余りのを下から列挙する
| 10進数25を2進数に変換する | 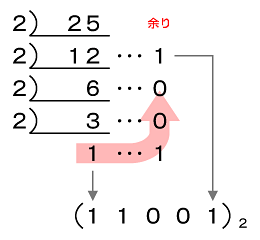 |
 2進数を10進数に変換する
2進数を10進数に変換する
2進数の値を下位の桁から順番に 20、21、22…を掛けてその結果を加える

 2進数から8進数or16進数、8進数or16進数から2進数
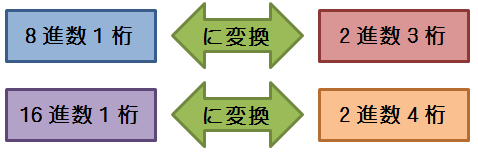
2進数から8進数or16進数、8進数or16進数から2進数
0から9までの10個の数字と、AからFまでの6個のアルファベットを使って数値を表現する方法。日常生活においては、0から9までの10個の数字を使った10進数が主に使われているが、コンピュータでは2進数などと並んで16進数を扱うことも多い。例えばASCIIコードや日本語の文字コード、色を示すカラーコードなどは16進数を使用している
符号付き2進数
2進数で負の数を扱う場合「符号付き2進数」を用いる。符号付き2進数では、最上位のビットが「0」の場合が+で、「1」の場合が−である
 ビット数に応じた表現できる値の範囲
ビット数に応じた表現できる値の範囲
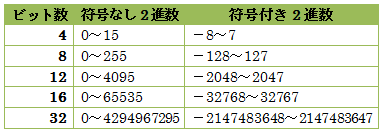
 符号付数値表現(ふごうつきすうちひょうげん)
符号付数値表現(ふごうつきすうちひょうげん)
コンピュータ内部での数値の正負(ゼロより大きいか小さいか)の表現方法
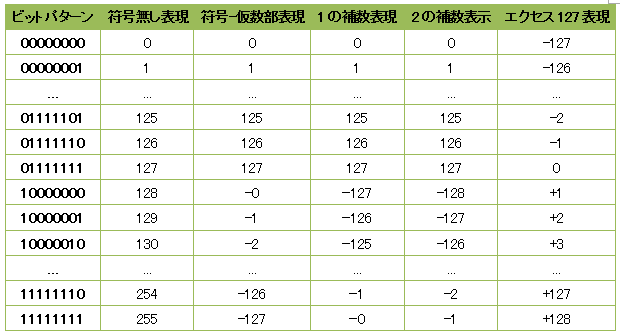
数学では、負の数はどういう場合でも一般的にマイナス記号「−」を数値の前に付けることによって表すことができる。しかし、コンピュータにとっては負の数を表す方法は一種類ではない。ここでは、二進記数法を拡張して負の数を表す方法を四種類説明する(符号-仮数部、1の補数、2の補数、エクセスN)
▼符号-仮数部
2進数に符号をつける問題を考えたときに最初に思いつくのが、符号ビットを追加して正負を表すことである。つまり符号ビット(一般に最上位ビット(MSB)を割り当てる)が0ならば正の数を示し、1ならば負の数を示す。他のビット列はその数値の仮数部(あるいは絶対値)となる。1バイトで数値を表す場合符号に1ビットを使うので、7ビットで表せる仮数部は 0000000 (0) から 1111111 (127) となる。したがって、1バイトで表せる数値は−12710 から +12710 となる。結果として、この表現方法では 0 の表現が二種類できてしまう(00000000 (0) と 10000000 (−0))。10進数の −43 はこの方式では 10101011 と表現される
▼1の補数
2進数における1の補数表現は、負の数の表現に正の数のビットを反転することで得られる。「符号-仮数部」表現のように、1の補数でも 0 には二種類の表現がある(00000000 (+0), 11111111 (−0))
例えば、00000011 (3) の1の補数は、11111100 (−43) である。1バイト幅で1の補数で表せる数値の範囲は −12710 から +12710 となる
▼2の補数
0が二種類の表現を持つという問題、キャリーを戻して加算しなければならない問題は、2の補数という体系を使うことで回避できる。2の補数では、負の数は1の補数より1だけ大きいビットパターンで表される。2の補数では、ゼロ(00000000)は一種類しかない。数値の逆数を得るには(元の数値が正か負かに関係なく)全ビットを反転させてから 1 を足せばよい
| 例1 | 例2 | |
| 1.右端から見ていき、最初の '1' を探す | 0101001 | 0101100 |
| 2.その '1' より左側のビット列を反転させる | 1010111 | 1010100 |
▼エクセスN
下駄ばき表現、あるいはオフセット・バイナリ(offset binary)とも呼ばれ、事前に決めたNという数をバイアス値として使う。ある数値は、元の値よりNだけ大きい符号無し数値として表現される。したがって、0 は N で表され、−Nはゼロが並んだビットパターンで表される
この表現は浮動小数点数で使われている。IEEE浮動小数点標準では単精度(32ビット)の指数部は8ビットのエクセス127として定義されている。 倍精度(64ビット)では11ビットのエクセス1023である
2進数の加算、減算
2進数の加算、減算を行う場合、桁を揃えて下の桁から計算する
 減算をする場合の裏ワザ
減算をする場合の裏ワザ
2の補数を加える ことによって減算をする
集合
ある条件に基づいてグループ化されたデータの集まりを「集合」と呼びます。「AまたはB」といったように言葉や文章で表現することがでる。こうした表現方法は「命題」と呼ばれている。また、命題された集合は「ベン図」により図式化することが可能
論理演算
論理演算は、1(真)か0(偽)かの2通りの入力値に対して1つの値を出力する演算。論理演算は、コンピュータ内部の演算に使用するほか、データベースの複数の語句を掛け合わせて検索する複合検索などにも応用される。論理演算で用いる集合の領域を表した図をベン図またはオイラー図と呼び、入出力の全てのパターンを表した表を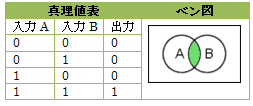 真理値表と呼ぶ
真理値表と呼ぶ
 論理積(AND)
論理積(AND)
AとBの両方を含む部分で、「AかつB」の関係を表す。入力値がすべて1の場合に1を出力し、それ以外の場合には0を出力します。この集合は、積集合や共通部分などとも呼ばれる
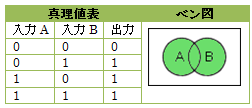
 論理和(OR)
論理和(OR)
AとBの少なくともいずれかを含む部分で、「AまたはB」の関係を表します。入力値のいずれかに1が入力された場合に1を出力し、それ以外の場合には0を出力します。この集合は、和集合や合併集合(Union)などとも呼ばれる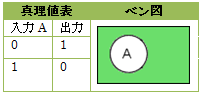
 否定(NOT)
否定(NOT)
Aを含まない部分で、「Aではない」関係を表します。入力された値が1なら0に、0なら1に反転します。この集合は、補集合(Compliment)などとも呼ばれる
 否定論理積(NAND)
否定論理積(NAND)
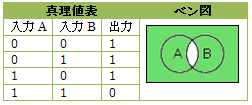
否定論理積(NAND)(Not And)は、論理積(AND)の出力を否定(NOT)したもので、「(AかつB)ではない」関係を表します。すべての入力値が1の場合に0を出力し、それ以外の場合には1を出力する
 否定論理和(NOR)
否定論理和(NOR)
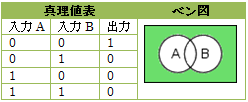
否定論理和(NOR)(Not Or)は、論理和(OR)の出力を否定(NOT)したもので、「(AまたはB)ではない」関係を表します。すべての入力値が0の場合に1を出力し、それ以外の場合には0を出力する
 排他的論理和(EOR、XOR)
排他的論理和(EOR、XOR)
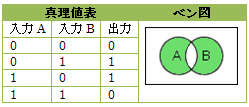
排他的論理和(EOR、XOR)(Exclusive Or)は、入力値が異なる場合に1を出力し、それ以外の場合(入力値が同じとき)には0を出力する
応用数学
データを収集し、業務上の問題分析を行うための手法のひとつに「応用数学」がある。「確率」や「統計」を駆使して、数学的な見地からの分析を行うことで、一定の裏付けを得ることができる
確率
収集したデータの総数や度合いを判断の材料とする手法。確率の基礎となる「順列」と「組合せ」は、全体の場合の数や条件を満たした場合の数を数え上げるための考え方として有効
順列
あるデータの集まりの中から任意の個数を取り出し、並べたときの並べ方の総数のこと

組合せ
いくつかの要素の集まりからいくつかの要素を選び出す方法、あるいは選び出した要素をその"並べる順番の違いを区別せずに"並べたもののこと

確率
ある現象が起こる度合い、ある試行が行われたあとある事象が現れる割合のことをいう。偶然性を含まないひとつに定まった数値であり、発生の度合いを示す指標として使われる

統計
収集したデーの規則性を調べたり、予測したりするための手法のこと
データの代表値
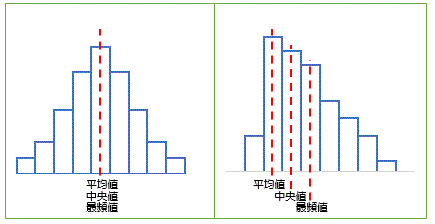
データ全体の特徴をひとつの数値で表現するもの
| 値 | 説明 |
|---|---|
| 平均値 | 全体の合計をデータ数で割った値のこと。一般的に"平均値"と呼んでいるものは、"算術平均"のこと |
| メジアン(中央値) | データを昇順、または降順に並べたときに中央に位置する値のこと。データが偶数の場合、中央に位置する2つの値の平均を使う |
| モード(最頻値) | データの出現度数の最も高い値のこと |
 |
データの散布度
個々のデータが平均値を中心に周囲の値がどのようにばらついているかの度合いを示す数値を表現する。同じ平均値を持つデータの集まりでも上のグラフのように特徴が異なる場合がある。この違い(変量がどのように散らばっているか)を表現する数値。各変量の平均からの隔たりが大きいか小さいかを調べる「分散」「標準偏差」変量の分布の幅、散らばり具合の幅が大きいか、小さいかを示す「レンジ」がある
| 値 | 説明 | 計算式 |
|---|---|---|
| 分散 | 標本が標本平均からどれだけ散らばっているか | ([個々のデータの値]−平均)を2乗した値の平均 |
| 標準偏差 | 統計値や確率変数の散らばり具合(ばらつき)を表す数値 | 分散の平方根を取ったもの |
| レンジ(範囲) | 変動・影響などの範囲。分布幅を示す数値 | データの最大値と最小値の差 |
正規分布
事象が起こる確率が変数によって決まる場合、変数と各事象が起こる確率との関係を「確率分布」といい、この変数を「確率変数」という。確率分布の代表的なものに、「正規分布」がある
正規分布とは、平均値の付近に集積するようなデータの分布を表した連続的な変数に関する確率分布である
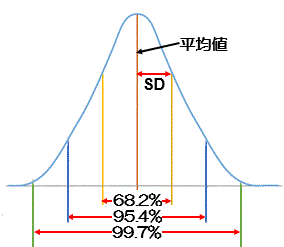
次のグラフで描いた曲線は、正規分布の曲線です。正規分布は次の特徴を持っている
・ 平均値を中心とした左右対称のつりがね型
・ 平均±1SD、±2SD、±3SDの確率−それぞれ68.2%、95.4%、99.7%
 ワークサンプリング法
ワークサンプリング法
観測回数を決めて、ランダムな瞬間に、ある作業者の作業状況を観測し、設備や作業時間などを分析する手法。「瞬間観測法」とも呼ぶ
情報に関する理論
情報量の単位
コンピュータの記憶容量を表す情報量の単位として「ビット」や「バイト」がある。この単位はコンピュータの性能や、メモリやハードディスクの容量などを知る際にも役立つ
ビットとバイト
ビットとバイトの関係は「8ビット=1バイト」であり、1ビットは2進数であるため、1バイトは2の8乗で256種類の情報を表現できる
情報量を表す単位
さらに大きな情報量を示す場合は、単位に接頭辞(接頭語)をつけて表現される。代表的な接頭辞としては、「K(キロ)」、「M(メガ)」、「G(ギガ)」、「T(テラ)」、「P(ペタ)」などがある。接頭語は単体で用いられることはなく、他の単位と組み合わせて利用される
| 単 位 | 読み方 | 意 味 |
|---|---|---|
| KB | キロバイト | 103=1000B(1KB=210=1024B) |
| MB | メガバイト | 106=1000KB(220=1024KB) |
| GB | ギガバイト | 109=1000MB(230=1024MB) |
| TB | テラバイト | 1012=1000GB(240=1024GB) |
| PB | ペタバイト | 1015=1000TB(250=1024TB) |
時間を表す単位
コンピュータの処理速度を表す時に用いられる、1秒未満の時間を表す単位は以下の通り
| 単 位 | 読み方 | 長 さ | 意 味 |
|---|---|---|---|
| ms | ミリ秒 | 1000分の1秒 | 1 ms=10−3s |
| μs | マイクロ秒 | 100万分の1秒 | 1μs=10−6s |
| ns | ナノ秒 | 10億分の1秒 | 1ns=10−9s |
| ps | ピコ秒 | 1000分の1ナノ秒 | 1ps=10−12s |
デジタル化(デジタル化)
歌声や楽器演奏、絵画などの情報は、アナログデータとして作成・表現されている。このような情報をコンピュータで扱うためには、データをデジタルの値に変換する必要がある。アナログデータのデジタル化により、コンピュータによる処理の対象となり、より効率的なデータの活用が実現できる。デジタル化のメリットとして、データを劣化させずオリジナルに近い状態で保持することや、コンピュータ処理による加工や複製、遠隔地とのデータ交換の実現などが期待できる
A/D変換
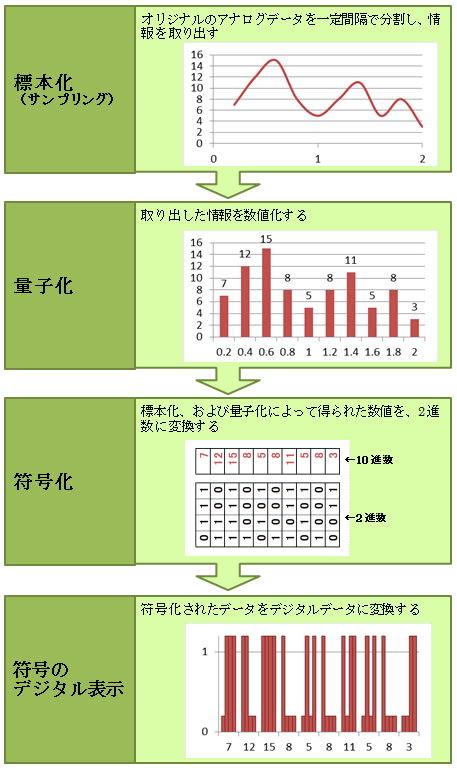
情報をアナログからデジタルへ変換することを「A/D変換」と呼ぶ。A/D変換では下記のようなステップを経て変換を行う
 エンコード
エンコード
データを一定の規則に基づいて変換すること。エンコードを行うソフトウェアを「エンコーダ」という
 デコード
デコード
エンコードされたデータから一定の規則に基づいて変換し、元のデータを取り出すこと。デコードを行うソフトウェアを「デコーダ」という
 サンプリングレート
サンプリングレート
1秒間にアナログデータを測定する回数のこと。「サンプリング周波数」とも呼ばれ、「Hz」で表す。サンプリングレートが大きいほど、デジタルデータで再現できる音質が良い
 サンプリングと量子化
サンプリングと量子化
アナログ信号は連続するデータで、デジタル信号は個々の途切れたデータである。A/D変換時に、サンプリングの周期を短くし量子化の段階を増やすことで、より細かく数値を採ることができアナログデータに近づけることができる
 デジタルデータの主な特徴
デジタルデータの主な特徴
| 項 目 | 内 容 |
|---|---|
| データの送信 | 遠隔地まで送信可能 |
| データの共有 | ネットワーク上でのデータ共有が可能 |
| データの画像処理 | 拡大・縮小、トリミングなどの加工・編集が可能 |
| データの画質 | 劣化しない |
| データの圧縮 | 可能 |
| データの検索 | 可能 |
| データのコピー | 可能 |
文字の表現
コンピュータでは文字を2進数の数値として扱っている。コンピュータ上で扱う文字に割り与えられた2進数コードを「文字コード」と呼んでいる
| 名 称 | 特 徴 |
|---|---|
| ASCII | 1バイト文字。1文字につき7ビットを使用し、8ビット目はエラー確認用のパリティ。欧文文字および欧文記号 |
| JIS | ひらがな、漢字等の2バイト文字を含む |
| シフトJIS | JISの一種。Microsoftによって定義された。WindowsやMac OSなどで採用されており、国内で最も普及している |
| EUC | AT&T社が規格。拡張UNIXコードともいう。主にUNIXで利用されている。2バイト文字にも対応している |
| EBCDIC | 米国IBM社が規格。8ビットの文字コード。主に汎用大型コンピュータで採用されている |
| Unicode | ISOとIECが規格。全世界の文字を2バイトで表現することで、1つのコードでほとんどの文字を収録している |

