暗号
暗号の基礎
暗号の概念
機密性を守るための暗号
インターネットでは、海外を含めていろいろなプロバイダを経由するので、誰かに盗聴されるという危険がある。
そこで、「暗号化」が必要となる。
(例)
オンラインバンキングを利用する → SSLという仕組みで通信を暗号化
パソコンのデータ → ファイル暗号化やディスク暗号化 → 不正な第三者にデータを読み取られるリスクが減る)
暗号に関する基本的な言葉
「平文(平文)」とは、暗号化されていない普通の文章のこと。これを「暗号鍵」を用いて「暗号化」することで、「暗号文」になる。逆に、「暗号文」を「復号鍵」を用いて元の「平文」に戻すことを「復号」と言いう。
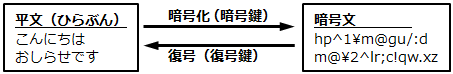
暗号化技術
古典的な暗号化方式
 転置式暗号
転置式暗号
一定の規則に基づいて順番を入れ替えて暗号文を生成する
(例:password → drowssap)
 換字式暗号
換字式暗号
一定の規則に基づいて別の文字や記号などに変換する
(例:password → drowssap → espxttbq)
※安全性の問題などから現在ではほとんど使用されていない
現在は・・・
 共通鍵暗号方式
共通鍵暗号方式
暗号化の鍵と復号の鍵が共通
 公開鍵暗号方式
公開鍵暗号方式
暗号化と復号に使用する鍵が異なる暗号方式
 ハイブリッド方式
ハイブリッド方式
共通鍵方式と公開鍵暗号方式の長所を組み合わせて作られている仕組み
共通鍵暗号方式
送信者と受信者で同じ鍵を使用する。
代表的な方式に「DES方式」「AES方式」がある
| ●暗号化と復号の速度が速い ●共通鍵の転送時に共通鍵が漏えいする危険性をともなう ●通信相手ごとに別々の共通鍵を用意する必要がある |

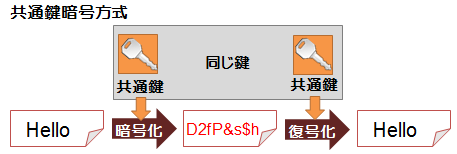
共通鍵暗号方式の種類
 ストリーム暗号
ストリーム暗号
ビット、バイト、文字単位で暗号化する
代表例:RC4
- キーストリーム(鍵ストリーム)と呼ばれる疑似乱数を暗号鍵として使用する
- ブロック暗号より処理を単純化できるため、処理速度が速い
- 暗号化してもデータサイズが増加しないため、通信での利用に適している
| アルゴリズム | 説明 |
|---|---|
| RC4 | ロナルド・リベスト氏が考案した1bit単位で暗号化・復号が可能なストリーム暗号 WEPやWPA、SSL/TLS、SSHで使用されている |
| SEAL | IBMで開発された方式で、米国で特許が成立している 高速処理が可能だが少量のデータ転送には不向き |
| MULTI-S01 | 日立製作所が開発した方式。米国製のPANAMAという疑似乱数発生器を使用する |
 ブロック暗号
ブロック暗号
ある程度の塊(ブロック)で暗号処理をする。
代表例:DES、3DES、AES
- ブロック単位で暗号処理を行うため、ブロックサイズ分のデータがそろうまで処理が開始できないので、待ち時間が発生する可能性がある
- ストリーム暗号より処理が複雑になる
- ブロックサイズは64ビットか128ビットが用いられる
| アルゴリズム | 鍵長 | 説明 |
|---|---|---|
| DES | 56bit | DES(Data Encryption Standard)という言葉の通り、かつての暗号(Encryption)の標準(Standard) |
| 3DES | 2-key(112bit) 3-key(168bit) | DESを3回繰り返す(三重に適用することで強度を強めた) |
| AES | 128bit,192bit 256bit から選択 | DESの脆弱性をカバーするために公募された暗号規格であり、Advanced Encryption Standardという言葉のとおり、次世代暗号標準という意味 |
| IDEA | 128bit | ブロック長は64bit。PGPやSSHで使用されている |
| FEAL | 64bit,128bit | NTTが開発した方式。ICカードや携帯電話などで使用されている ブロック長は64bit |
| MISTY | 128bit | 三菱電機が開発した方式。携帯電話のW-CDMA用暗号KASUMIのベース。ブロック長は64bit |
| RC2 | 可変長 (最大128bit) | ロナルド・リベスト氏が開発した方式。ブロック長は64bit |
| RC5 | 可変長 | ロナルド・リベスト氏が開発した方式。ブロック長、鍵長共に可変 |
※段数※
●変換をn回実施。このnが段数。
●鍵長によって、段数が決まるのがAESの特徴でもある。
ちなみに、AESは鍵長128bitで18段、192と256bitで24段。
 利用モード
利用モード
ブロック暗号アルゴリズムを用いてブロック長よりも長いデータを暗号化する際に使われる技術のこと。ブロック暗号では、各ブロックを単純に同じキーとアルゴリズムを用いて暗号化した場合、頻度などから暗号が解かれやすくなる。そこで、単純なブロック単位の暗号(ECB:Electronic Codebook)ではなく、前のブロックの暗号情報を使って暗号化する(CBC:Cipher Block Chaining)が、DESやAESで利用されている。
AES、DESなどのブロック暗号を用いる暗号化では、入力文(平文)は固定長の短いブロックに分割されて処理される。このとき、各入力ブロックを暗号化する際に様々な形式でフィードバックデータを用いる次のような暗号利用モードが定義されている。
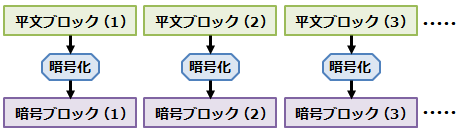
 ECB (Electronic Code Block) モード
ECB (Electronic Code Block) モード
- フィードバックを行なわず、入力ブロックをそのまま暗号化するモードで、入力文と鍵が同じならば常に同じ暗号文が生成される。
- 単一ブロックの短いランダムなデータの暗号化にのみ利用される。
- ビット損失などによりブロック境界が失われると、復号は失敗する(再同期が必要)。
 CBC (Cipher Block Chaining) モード
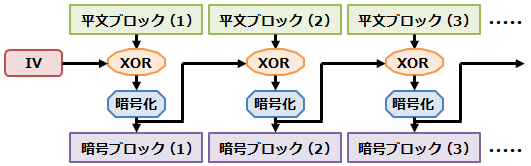
CBC (Cipher Block Chaining) モード
- 各ブロックの暗号化処理に、直前の入力ブロックの暗号化によって得られた暗号ブロックを利用する(入力ブロックと暗号ブロックの排他的論理和を取る)。フィードバックデータとして、直前の暗号ブロックを用いる。最初のブロックに対しては、初期ベクトル(IV)を暗号ブロックとして与える。
- 初期ベクトルが異なれば同じ鍵でも異なる暗号文が得られる。
- 単一暗号ブロック内の伝送ビット誤りは、2つの復号ブロックに影響を与える。
- ビット損失などによりブロック境界が失われると、復号は失敗する(再同期が必要)。
- メッセージ認証が可能である。
- 暗号通信(ISO8732)、暗号FAXなどに利用される。
 CFB (Cipher FeedBack) モード
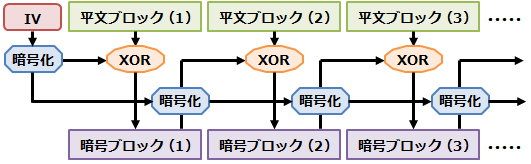
CFB (Cipher FeedBack) モード
- 直前の暗号ブロックを暗号化したものと入力ブロックの排他的論理和を取り暗号ブロックとする。この暗号ブロックをさらに暗号化して次の入力ブロックと結合する処理を繰り返す。フィードバックデータは、直前の暗号ブロックを暗号化したものになる。
- 同期の必要がない(自己同期)。
- メッセージ認証が可能である。
- 回線暗号装置(ISO9160)などに利用される。
 OFB (Output FeedBack) モード
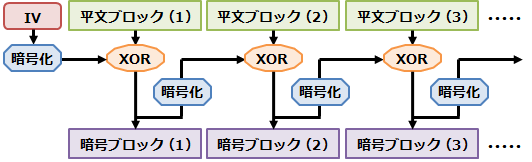
OFB (Output FeedBack) モード
- 初期ベクタを暗号化することによって得られるデータ(フィードバックデータ)を最初の入力ブロックと排他的論理和を取り暗号とする。さらに、このフィードバックデータを暗号化して次の入力ブロックと結合し次の暗号ブロックとする処理を繰り返す。 フィードバックデータは、初期ベクタを繰り返し暗号化したものになる。
- メッセージに関係なく事前計算ができる。
- ビット損失に対して再同期が必要である。
- ビット誤りに対して影響が伝播しない(画像通信,AV暗号システムなどに利用される)。
 CTR (Counter) モード
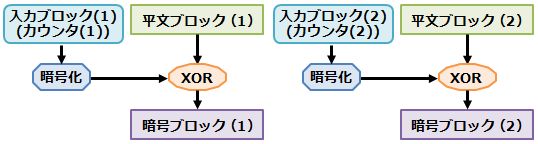
CTR (Counter) モード
- カウンタと呼ばれる一連の入力ブロックを暗号化することによって得られるデータと平文とを排他的論理和を取り暗号とする。
- カウンタの暗号化は、平文または暗号文に関係なく事前に計算ができる。
- カウンタの暗号化は、カウンタ値が決定されているならば、各ブロック独立かつ並列に実行できる。
ECBとCTRモード以外は最初のブロックの暗号化に初期ベクタと呼ばれるブロック長と同サイズの初期値を指定する。入力文と鍵が同じでも、この初期ベクタ値を変えることにより異なった暗号文が得られるため、暗号文解析が難しくなる。初期ベクタ値は暗号化と復号で同一の値を用いるが、鍵と異なり秘密としなくても安全性は損なわれない。
CTRモードでは、一連のカウンタ値を指定する必要がある。
公開鍵暗号方式
暗号化と復号に使用する鍵が異なる暗号方式。暗号化に使用する鍵を公開した方式。受信者の公開鍵を入手すれば、誰でも受信者に暗号文を送れるが、暗号文を復号化できるのは、公開鍵とペアになる秘密鍵を持つ受信者だけ。代表的な方式に、RSA暗号方式がある
| ●公開鍵を使うため、多数の送信相手と通信するのに適している ●鍵の管理が容易である ●暗号化と復号の速度が遅い |
★必要な鍵の数=2n

| RSA | 公開鍵暗号方式の標準として広く普及している。桁数の大きな整数の素因数分解の困難さを利用、安全性の根拠にしている。1024ビットの鍵が標準的に使用されていたが、危殆化が懸念され、2048ビット以上の鍵への移行が進められている |
|---|---|
| 楕円曲線暗号 (ECC) | 楕円曲線上の離散対数問題(EC-DLP)の困難性を安全性の根拠とする暗号。RSA暗号などと比べて、同レベルの安全性をより短い鍵で実現でき、処理速度も速いことがメリット。条件の選び方によっては逆に脆弱になってしまうという欠点がある。160ビットの鍵長で鍵長1024ビットのRSAと同程度の安全性を持つとされる。 |
- 公開鍵暗号方式を用い、送受信メッセージを暗号化して盗聴されないようにしたい。送信時にメッセージの暗号化に使用する鍵は・・・
送信先の公開鍵(受信者の公開鍵)
- 公開鍵暗号方式の用法によって、送信者が間違いなく本人であることを受信者が確認できる鍵の組み合わせは・・・
送信者の秘密鍵で暗号化し受信者は送信者の公開鍵で復号する
→送信者のみが知る鍵で暗号化し、復号確認されなければならない。
ハイブリッド暗号方式
共通鍵方式と公開鍵暗号方式の長所を組み合わせて作られている仕組み
|
●処理が高速 ●鍵の管理・配布が容易 ●送信者が共通鍵を任意に作る ●その鍵を受信者の公開鍵で暗号化して送る |
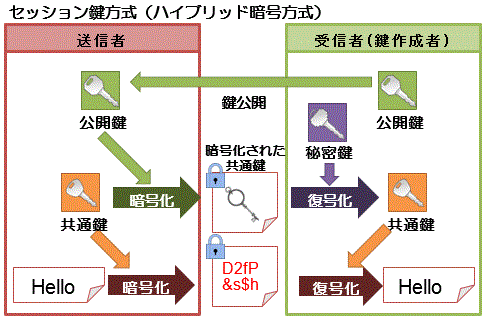
例)メールを暗号化する仕組みであるS/MIME
- 電子メールで公開鍵暗号方式を使用し、鍵の生成はセキュリティ部門が一括しておこなっている場合、秘密鍵の適切な保管方法は・・・
暗号化された秘密鍵の一つ一つを分割し、複数のセキュリティ管理者が分担して保管する。
ハッシュ関数
ハッシュ関数とは、任意の長さの入力データをもとに、固定長のビット列、ハッシュ値(メッセージダイジェスト)を作成するもので、メッセージダイジェストは文書の短編版。ハッシュ関数にはMD5やSHA-1があるが、これらに危殆化の問題があり、SHA-2などが利用されるようになっている。
※hashとは、「細切れにする」という意味
【特 徴】
- どんな長さのデータも必ず固定長になる
- 同じメッセージからは同じハッシュ値が出力される
- メッセージがほんの少しでも異なれば、出力されるハッシュ値は大きく異なる
- ハッシュ値から元のメッセージを求めることはほぼ不可能
(メッセージダイジェストからメッセージを求めることはほぼ不可能)
| MD4 | 一方向性ハッシュ関数。128ビットのハッシュ値を出力する。S/Keyなどで使用されていたが、アルゴリズムにいくつかの欠点が発見され、現在ではMD5が主流となっている |
|---|---|
| MD5 | 一方向性ハッシュ関数。MD4同様、128ビットのハッシュ値を出力する。MD4のアルゴリズムを複雑化して安全性を向上させた。SHA-1とともに広く使用されている。 |
| SHA-1 | 一方向性ハッシュ関数。160ビットのハッシュ値を出力する。米国政府標準のハッシュ関数として採用されたこともあり、広く使用されていたが、近年危殆化が懸念され、SHA-2、SHA-3への移行が進められている。 |
| SHA-2 | 前規格であるSHA-1から多くの改良が加えられている。SHA-2にはSHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256の6つのバリエーションがあり、ハッシュ値は"-"(ハイフン)の後の数字、224, 256, 384, 512ビットである。 |
| SHA-3 | 元はKeccakとして知られた暗号学的ハッシュ関数(NISTによる次世代暗号コンペティションの結果、選出された)。SHA3-nおよびKeccak-n において、n = 224, 256, 384, 512は出力ハッシュ値である。 |
ハッシュ関数Hash(key)は、keyを基にデータの格納位置を算出して、戻り値として戻す。格納位置は1~Nの整数となる。関数Hash(key)が、異なるkeyから同じ格納位置を算出することを、シノニムの発生という。
- シノニム(または衝突:collision)
違うキーの値でも、ハッシュ関数を適用した結果が同じ値になること
- シノニムレコードのキー値の計算
剰余が同じものを探す
例)4,999を除数とする剰余を用いるハッシュ関数で、
キー値が12,500のレコードに対するシノニムレコードのキー値はどれか。
ア.2
イ.1,250
ウ.2,501
エ.17,499
剰余が同じものを探す。
12500 ÷ 4999 = 2 あまり2502
2 ÷ 4999 = 0 あまり2
1250 ÷ 4999 = 0 あまり1250
2501 ÷ 4999 = 0 あまり2501
17499 ÷ 4999 = 3 あまり2502
よってエ
≪ハッシュ関数とソルト≫
パスワードを暗号化するために利用されているハッシュ関数。ハッシュ値から元のパスワードデータを復元することができないというのが、ハッシュ関数の特徴だが、少ない文字数のパスワードであれば、現在のコンピュータ性能であれば、復元可能!
しかし、パスワードの情報だけでなく、ソルトという情報を付加してハッシュ値を計算することによって、ハッシュ値からパスワードを特定しにくくする方法がある
★パスワードの保存方法★
ユーザ認証用のパスワードは、認証サーバにて、そのままの平文で保存されているわけではない。ハッシュ値によって暗号化されている。

しかし、以下のように、パスワードとハッシュ値をデータベース化(レインボーテーブル)し、不正入手したパスワードのハッシュ値から元のパスワードを見つけることが可能。

そこで、ソルトを使用する。パスワードをハッシュするときに、ランダムな値(ソルト)を付加することにより、同じパスワードでも、ソルトが違うので、ハッシュ値も違う。攻撃者はレインボーテーブルを用意できなくなる
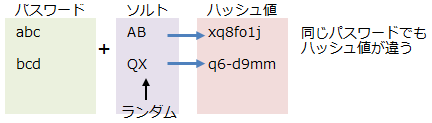
★★ソルトを使用するとハッジュ値からパスワードを特定しにくくなる
・同じパスワードでもソルトが異なるとハッシュ値が変わるから
・攻撃者がソルトの値ごとにテーブルを用意する必要があるから
- 暗号アルゴリズムの危殆化
計算能力の向上などによって、鍵の推定が可能となり,暗号の安全性が低下すること
暗号方式には寿命がある。
それは、NISTが定めた、米国政府機関のコンピュータシステムの調達基準のことで、表に示す暗号アルゴリズムを利用したシステムなどの調達は2010年までしか認められていない。
米国政府調達基準で現在調達可能で2011年以降調達できなくなる暗号アルゴリズム
| 分類 | 名称 |
|---|---|
| 共通鍵暗号 | 2-key Triple DES |
| 公開鍵暗号 | 鍵長1024ビットのRSA 鍵長160ビットのECDSA |
| ハッシュ関数 | SHA-1 |
- コンピュータの性能が上がることによって、数年後には、現在広く利用されている、鍵長1024ビットのRSA公開鍵から秘密鍵が推測される可能性があり、電子署名の対象のデータの改ざんやなりすましが行われる可能性があり、鍵長を更に長くすることが求められる。
- ハッシュ関数として現在広く利用されているSHA-1には、ある条件下でハッシュ値の衝突を意図的に起こすことができる、という脆弱性が発見されていて、脆弱性を攻撃されると、電子署名の信頼性が損なわれる。
- 電子透かし
- 画像などのディジタルコンテンツが、不正にコピーされて転売されたものであるかを判別できる対策
- 最近では、フリーソフトなどでも電子透かしを入れることができます。
- ステガノグラフィの技術を利用したものです
- ステガノグラフィ
- メッセージを画像データや音声データなどに埋め込み、メッセージの存在を隠す技術
- 「電子透かし」と「ステガノグラフィ」別物、ステガノグラフィは、暗号技術。
MAC(message authentication code)
メッセージ認証にて、メッセージが改ざんされていないかの確認に使われる。
送信者と受信者の共通鍵を元に、MACアルゴリズムを適用して生成したもの
MACアルゴリズムは、入力として共通鍵と認証すべき任意長のメッセージを受け取り、MAC(「タグ」とも呼ばれる)を出力する。
MACアルゴリズムは他の暗号プリミティブから構築でき、ハッシュ関数を使う方式(HMAC)、ブロック暗号アルゴリズムを使う方式(OMAC/CMAC、CBC-MAC、PMAC)などがある。
 実現できること
実現できること
- データの正真性のチェック
- 認証
 弱点
弱点
- 否認防止ができない
 メッセージ認証コードの例
メッセージ認証コードの例
- HMAC
 仕組み
仕組み
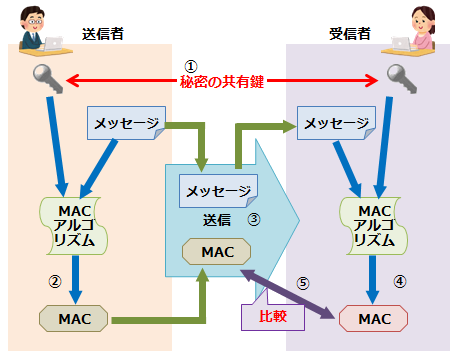
①送信者と受信者は、あらかじめ秘密の共通鍵を共有しておく。
②送信者は、元データと鍵からMACを計算する。
③送信者は、元データとMACを受信者に送る。
④受信者は、受信した元データと鍵からMACを計算する。
⑤受信者は、受信したMACと計算したMACを比較する。
(両者が一致すれば、改ざんされていない)
HMAC (Hash-based Message Authentication Code)
メッセージ認証符号 (MAC; Message Authentication Code) の一つであり、秘密鍵とメッセージ(データ)とハッシュ関数をもとに計算される。メッセージ本体と秘密鍵を一定の規則に従って組み合わせハッシュ関数に与え、算出されたハッシュ値を認証符号とするもの。ハッシュ関数は様々なものを使用でき、「HMAC-MD5」「HMAC-SHA256」のように末尾にハッシュ関数の種類を付加する。
フィンガプリント(拇印、指紋)
ディジタル証明書、公開鍵、メールなどの電子データが改ざんされていないことを証明するために使用データ。ハッシュ関数を用いて対象となる電子データから生成する。
例)公開鍵 公開鍵のハッシュ。
政府認証基盤(GPKI) ブラウザの拇印を確認する
ことで、検証することが可能。
インターネットを経由せずに、相手から紙媒体で入手するのが望ましい。
- メールの署名
メールの署名に以下のように付いている

- ブラウザ
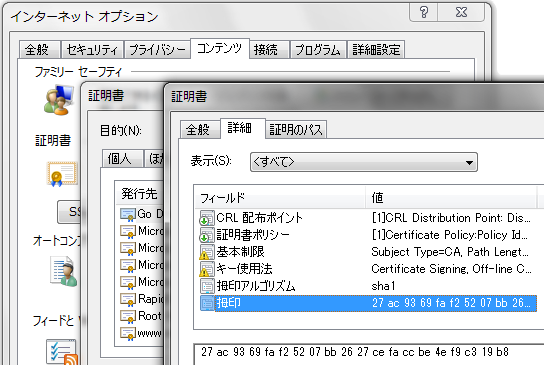
ブラウザに証明書が入れられているのであれば、ブラウザから確認可能。
[インターネットオプション][コンテンツ][証明書]で該当の証明書を開く。[詳細]タブの[拇印]で確認できる。
DH(Diffie-Hellman)法
安全でない通信経路を利用する両者が、秘密の共通かぎを安全に共有する方式
IPsecなどで使用されている。
手順
例)
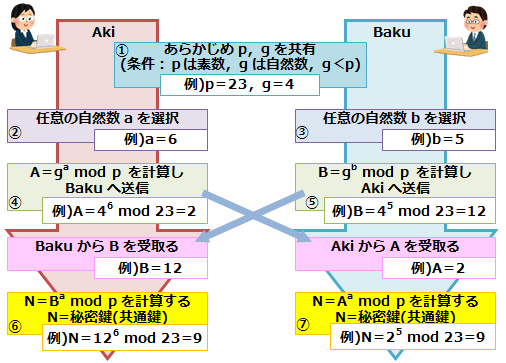
①利用者AkiとBakuは素数pと、pよりも小さいある自然数gを共有している
②Akiは、pより小さい任意の自然数aを選択する
③Bakuもpより小さい任意の自然数bを選択する
④Akiは以下の式で得られるAをBakuへ送信する
A=ga mod p (x mod yは整数xを整数yで割った余り)
⑤Bakuは以下の式で得られるBをAkiへ送信する
B=gb mod p
⑥Akiは受取ったBを使って、以下の式で秘密鍵Nを得る
N=Ba mod p
⑦Bakuは受取ったAを使って、以下の式で秘密鍵Nを得る
N=Ab mod p
注意点
- この方式の安全性はほかの公開かぎ暗号と同じく計算の一方向性に基づいている。DH法において、素数pの値が十分に大きい場合、秘密鍵から公開鍵を求めるのは容易であるが、公開鍵から秘密鍵を求めるのは非常に困難である。反対に、素数pの値が小さい場合には、鍵の値が小さくなるので公開鍵から秘密鍵を短時間で求めることも可能であり、安全性に問題がある。
- DH法は、通信経路上の第三者Cが、利用者Aから送られる情報を、にせの情報にすりかえて利用者Bに送信する中間者攻撃に対して弱い。中間者攻撃を防ぐためには公開鍵に信頼できる第三者によるディジタル署名をつけるなどの対策が必要である。
- 第三者Cが暗号文を傍受してそれを手掛かりとして共通鍵を見つけるリスクもあるので、継続的な通信の安全性を高めるための対策として、共通鍵の値が十分に大きいものを使うだけでなく、共通かぎの更新間隔の短縮も有効
暗号分野におけるゼロ知識証明とは、相手に秘密情報そのものを送ることなく、自分が該当秘密情報を知っていることを相手に伝える方法
米国の規格、暗号の仕組みの基準。セキュリティ製品のセキュリティ要件のガイドラインみたいなもの。
「暗号モジュールのセキュリティ要求事項」
「モジュール」はハードやソフトなどをひっくるめたもの。
PCに内蔵されるセキュリティチップのこと
鍵ペアの生成する機能がある
セキュリティチップにて、パソコンハードディスクを暗号化すると、ハードディスクを持ち出されても復号することはできない。

